Разработка и применение программного обеспечения в физических исследованиях
Вячеслав Федоров, ИЯФ СО РАН
Для студентов физических специальностей и начинающих ИТ-специалистов, которые хотят познакомиться с Python, Linux, DevOps и SRE.
Цель этой книги — помочь тебе научиться писать более красивые, надёжные и легко сопровождаемые программы для физических исследований. То, о чём мы здесь будем говорить, это не начальный уровень, предполагается, что ты уже знаешь основы физики, минимально умеешь программировать, и хочешь научиться делать это лучше.
И это — отличная цель, к которой мы вместе будем двигаться!
Часто на физических факультетах не уделяется должного внимания IT-дисциплинам, в то время как они очень важны и могут значительно улучшить качество твоих исследований.
В ревью кода моих коллег часто видны результаты того, что в учебных материалах не уделяется отдельное внимание вопросам качества кода. Качество программы и её надёжность страдают — а это гораздо более важные параметры, чем многие поначалу думают. Поначалу кажется, что я написал программу, она в моих идеальных условиях работает и этого достаточно. Но нет, этого недостаточно. Наличие функциональности это одно, а надёжность этой функциональности и качество реализации этой функциональности это совсем другое. То, что мы написали программу и она имеет функциональность — это вовсе не означает, что программа действительно хороша. В этой небольшой книге мы поговорим о том, как разрабатывать, думая не только о функциональности, но и о качестве и надёжности её реализации.
Цели книги:
- Познакомиться с основами Linux: Изучить архитектуру операционной системы GNU/Linux, файловые системы, процессы загрузки и методы управления дисками.
- Освоить Python: Погрузиться в мир программирования на Python, изучить синтаксис, использование интерактивной оболочки IPython и применять язык для решения физических задач.
- Изучить DevOps и SRE: Разобраться в жизненном цикле программного обеспечения, управлении версиями, автоматизации процессов разработки и обеспечения надежности систем.
- Научиться работать с базами данных: Понять различные системы управления базами данных (СУБД) и их применение в реальных проектах.
- Освоить инструменты для обработки и анализа данных: Изучить библиотеки NumPy, SciPy, Pandas, Matplotlib и другие для эффективного анализа больших данных.
- Погрузиться в машинное обучение и нейронные сети: Изучить базовые алгоритмы классификации и основы работы с нейронными сетями для обработки данных физических экспериментов.
- Оптимизировать производительность программ: Научиться измерять время выполнения кода, использовать параллельные вычисления и работать с GPU для ускорения обработки данных.
Общие знания
Введение в алгоритмы
Одна из основных задач при работе с алгоритмами — оценка эффективности программы и поиск наиболее экономичного подхода. Самое простое и поверхностное решение этой задачи — написать программу и замерить время её выполнения. Программа тормозит? Изменить программу, оптимизировав решение.
Линейный поиск
Дан массив целых чисел длины $N$. Нужно найти в нём заданное число $x$ и вернуть его индекс. Если $x$ в массиве не встречается — вернуть -1.
def find_element(numbers, x):
for i in range(len(numbers)):
if numbers[i] == x:
return i
return -1
Можем сказать, что скорость работы алгоритма в худшем случае пропорциональна размеру массива. На математическом языке ещё говорят: «Вычислительная сложность алгоритма линейно зависит от размера входных данных».
Разберём эту фразу:
Вычислительная сложность алгоритма. Обычно под этой фразой понимают количество элементарных операций, которые будут совершены.
Размер входных данных. Входные данные — то, что алгоритм получает на вход. В нашей задаче это массив numbers и переменная x. Размер входных данных примерно равен N.
Линейная зависимость. Описывается формулой $y = kx+b$.
Бинарный поиск
Есть и другой способ решить задачу поиска элемента в массиве. Если элементы в массиве упорядочены по возрастанию, то найти нужный можно гораздо быстрее.
Допустим, мы хотим применить этот алгоритм к словарю из 100 страниц. Объём рассматриваемой части книги будет каждый раз уменьшаться вдвое до тех пор, пока не останется всего одна страница. Делить словарь из 100 страниц пополам мы можем максимум 7 раз. Получается, чтобы найти нужное слово, нам достаточно будет просмотреть не более 7 страниц.
Рассмотренный алгоритм называется бинарным поиском. Ещё его называют: двоичный поиск, метод деления пополам, дихотомия. Скорость его работы имеет логарифмическую зависимость от размера входных данных.
def binary_search(arr, x):
mid, low, high = 0, 0, len(arr) - 1
while low <= high:
mid = (high + low) // 2
if arr[mid] < x:
low = mid + 1
elif arr[mid] > x:
high = mid - 1
else:
return mid
return -1
Линейный vs Бинарный поиск
Запустим линейный и бинарный поиск на одинаковых данных и посмотрим, как меняется время работы в зависимости от размера массива, в котором производится поиск:
| Размер массива | Линейный поиск | Бинарный поиск |
|---|---|---|
| 10 элементов | 0.01 с. | 0.01 с. |
| 100 элементов | 0.1 с. | 0.02 с. |
| 1 000 элементов | 0.9 с. | 0.03 с. |
| 10 000 элементов | 9.75 с. | 0.06 с. |
| 100 000 элементов | 67.25 с. | 0.45 с. |
arr = [x for x in range(10_000)]
x = 999
%timeit find_element(arr, x)
37.4 µs ± 1.98 µs per loop (mean ± std. dev. of 7 runs, 10,000 loops each)
%timeit binary1.39 µs ± 44 ns per loop (mean ± std. dev. of 7 runs, 1,000,000 loops each)1.39 µs ± 44 ns per loop (mean ± std. dev. of 7 runs, 1,000,000 loops each)_search(arr, x)
1.39 µs ± 44 ns per loop (mean ± std. dev. of 7 runs, 1,000,000 loops each)
Сложность алгоритма. О-нотация
В О-нотации не учитываются константы и коэффициенты. То есть если в алгоритме совершается $5\cdot n+3$ операций, его сложность будет $O(n)$. В асимптотической оценке не учитываются значения констант при $n$. Нельзя сказать, что константы совсем уж не важны, но они не могут принципиально изменить применимость алгоритма на практике.
Кроме линейной и логарифмической, при оценке времени работы алгоритмов часто встречаются ещё такие зависимости:
- Квадратичная зависимость — $O(n^2)$.
- Кубическая зависимость — $O(n^3)$.
- Экспоненциальная зависимость — $O(2^n)$.
- Константная зависимость — $O(1)$. Бывает и так, что время работы алгоритма не зависит от размера входных данных, и в любом случае выполняется константное количество операций.
Как оценивать время исполнения
Теперь нужно понять, как быстро работает компьютер. Современный процессор выполняет около 2.5 миллиардов действий (их называют «инструкциями») в секунду. Или «тактовая частота процессора = 2.5 ГГц».
Если говорить немного точнее, за секунду проходит 2.5 миллиарда тактов. Как метроном задаёт ритм музыки, так же специальный генератор тактовой частоты задаёт ритм, в котором работают процессор и микросхемы компьютера. В первом приближении можно считать, что один такт соответствует одной инструкции.
Предположим, что обработка каждой итерации цикла занимает один такт процессора. Возьмем $10^9$ итераций, тогда:
$$ t = \frac{10^9 [итер] \cdot 1 [\frac{такт}{итер}]}{2.5 \cdot 10^9 [\frac{такт}{с}]} = 0.4 [с] $$
Количество инструкций в программе может немного отличаться в зависимости от процессора или от использованного компилятора. Бывают команды, которым требуется несколько тактов, а другие инструкции, наоборот, справляются за доли такта.
Получается, даже если бы мы хотели узнать константы в оценке временной сложности алгоритма, мы бы не смогли это сделать — слишком много нюансов пришлось бы учесть. Это ещё одна причина, почему мы пользуемся О-нотацией и опускаем константы. Но это не значит, что нельзя уменьшить константу, сократив число действий.
Чтобы оценить, во сколько раз мы ошиблись в действительности, измерим, сколько секунд займёт цикл, который миллиард раз не делает ничего.
# Python
import time
time_start = time.time()
i = 0
while i < 1000000000:
# Do nothing
i += 1
time_finish = time.time()
time_span = time_finish - time_start
print(time_span, 'seconds')
97.01491403579712 seconds
// CPP
#include <chrono>
#include <iostream>
int main() {
using namespace std::chrono;
auto time_start = high_resolution_clock::now();
int i = 0;
while (i < 1000000000) {
// Do nothing
++i;
}
auto time_finish = high_resolution_clock::now();
auto time_span = duration_cast<duration<double>>(time_finish - time_start);
std::cout << time_span.count() << " seconds\n";
return 0;
}
Каждая итерация цикла состоит из трёх действий: прибавить единицу, проверить условие и переместиться обратно к началу цикла. Три миллиарда команд должны занимать приблизительно 1 секунду. Программа на C++ работает почти столько же времени. А вот аналогичная программа на Python выполняется около 100 секунд, то есть в сто раз медленнее. Так происходит, поскольку код на языках низкого уровня почти один к одному транслируется в инструкции процессору.
Пространственная сложность алгоритма
Поговорили про понятие вычислительной (или временнóй) сложности, которое определяет, насколько эффективно алгоритм использует процессорное время. Ещё одна важная характеристика — объём оперативной памяти. Программы, которым не хватает памяти, будут зависать и мешать работе других программ. А во многих случаях и вовсе не смогут доделать свою работу до конца.
Если программе не хватает оперативной памяти, она пытается использовать файл подкачки, или swap-раздел (от англ. swap — «подкачивать»), расположенный во внешней памяти (на жёстком диске или на SSD-диске). При недостатке оперативной памяти программа начинает перекладывать данные из небольшой, но быстрой оперативной памяти на большой, но медленный диск. И по мере необходимости возвращать требуемые данные с диска в память. Это очень медленный процесс. Именно из-за него программы, вышедшие за пределы оперативной памяти, начинают тратить много процессорного времени и зависать, даже если у них небольшая временна́я сложность. И, что ещё хуже, они могут вытеснять из памяти другие программы, которые в таком случае тоже зависают. Если запущенные на компьютере программы заняли не только всю оперативную память, но и файл подкачки, то какая-то из программ завершится аварийно.
Каждый объект в программе занимает некоторый объём памяти, а для хранения всех объектов может потребоваться немало пространства. Особенное внимание, конечно, следует уделять массивам, строкам и прочим контейнерам, ведь их размер не строго фиксирован и зависит от входных данных. Пространственной сложностью алгоритма называется зависимость объёма потребляемой памяти от входных данных. Как и в случае с временной сложностью, нас в первую очередь интересует не точный объём памяти, а асимптотика, то есть скорость роста без учёта констант и коэффициентов.
Взаимосвязь пространственной и временной сложности алгоритма
Типичная ситуация: мы сохранили вспомогательную информацию, чтобы тратить меньше времени, то есть «обменяли» память на скорость. При решении задач вам порой придётся делать непростой выбор: либо сохранять больше данных, чтобы уменьшить объём вычислений; либо считать медленнее, но сэкономить память. Следует помнить о том, что слишком большой расход памяти может привести к тому, что программа завершится с ошибкой. Или её производительность ухудшится из-за использования файла подкачки.
Как тестировать свою программу
Код, разделённый на функции, удобно тестировать. Для тестирования отдельных функций пишут юнит-тесты.
Краевые случаи:
| тип теста | строки | числа | набор данных/массивы |
|---|---|---|---|
| самый маленький тест | пустая строка | 0 или минимальное отрицательное число для задачи | пустой набор данных |
| самый большой тест | самая длинная строка по условию | самое большое положительное число для задачи | набор данных максимального размера |
| особые случаи | строки со строчными и заглавными буквами строки с кириллицей и латиницей | положительное/отрицательное число ноль четное/нечет число вещественное число | набор с одинаковыми элементами отсортированные наборы неотсортированные наборы |
Задача
Дана строка (UTF-8). Найти самый часто встречающийся в ней символ.
Решение 1
Переберем все позиции и для каждой позиции в строке еще раз переберем все позиции и в случае совпадения прибавим к счетчику единицу. Найдем максимальное значение счетчика.
s = 'ababa'
ans = ''
anscnt = 0
for i in range(len(s)):
nowcnt = 0
for j in range(len(s)):
if s[i] == s[j]:
nowcnt += 1
if nowcnt > anscnt:
ans = s[i]
anscnt = nowcnt
print(ans)
a
Решение 2
Переберем все символы, встречающиеся в строке, а затем переберем все позиции и в случае совпадения прибавим к счетчику единицу. Найдем максимальное значение счетчика.
s = 'ababa'
ans = ''
anscnt = 0
for now in set(s):
nowcnt = 0
for j in range(len(s)):
if now == s[j]:
nowcnt += 1
if nowcnt > anscnt:
ans = now
anscnt = nowcnt
print(ans)
a
Решение 3
Заведем словарь, где ключом является символ, а значением - сколько раз он встретился. Если символ встретился впервые - создаем элемент словаря с ключом, совпадающем с этим символом и значением ноль. Прибавляем к элементу словаря с ключом, совпадающем с этим символом, единицу.
s = 'ababa'
ans = ''
anscnt = 0
symcnt = {}
for now in s:
if now not in symcnt:
symcnt[now] = 0
symcnt[now] += 1
if symcnt[now] > anscnt:
ans = now
anscnt = symcnt[now]
print(ans)
a
Сравнение сложности
N - длина строки, К - кол-во различных символов
| Решение | Время | Память |
|---|---|---|
| 1 | О(N^2) | О(N) |
| 2 | О(NK) | O(N+K) = O(N) |
| 3 | O(N) | O(K) |
Зачем программисту алгоритмы
- Знание алгоритмов помогает эффективному решению задач
- Дополнительная готовность к собеседованию
- Общая когнитивная тренировка
Свойства алгоритмов
- Дискретность
- Детерминированность
- "Понятность"
- Завершаемость
- Массовость
- Результативность
Лайфхаки. Оценка сложности
- Видишь цикл - сложность линейная
- Видишь вложенный цикл - сложность полиномиальная, степень - глубина вложенности
- Видишь деление пополам - сложность логарифмическая
- Видишь полный перебор - сложность экспоненциальная
Есть ли неразрешенные алгоритмические проблемы
Проблема останова
- Допустим, что у нас есть алгоритма $A$ и входные данные $N$. Нужен такой алгоритм, который скажет, остановится ли $A$ на входных данных $N$.
- Доказательство: от противного с подачей этого алгоритма на вход самому себе
Ресурсы
- https://tproger.ru/digest/competitive-programming-practice/
- Введение в анализ сложности: https://habr.com/ru/post/196560/
- Гейл Макдауэлл «Карьера программиста»
Бонус. Задача. Поиск простых чисел
def is_prime(n):
if n == 1:
return False
i = 2
while i < n:
if n % i == 0:
return False
i = i + 1
return True
Можно решить эту задачу быстрее. Проверять числа, которые больше чем $\sqrt n$, необязательно.
def is_prime(n):
if n == 1:
return False
i = 2
while i * i <= n:
if n % i == 0:
return False
i = i + 1
return True
C помощью функции is_prime(n) можно найти все простые числа, не больше числа $n$.
Для этого заведём пустой массив smaller_primes. Будем проверять все числа, меньшие или равные $n$, на простоту. Если число простое, добавим его в массив smaller_primes. В конце работы алгоритма в этом массиве будет содержаться ответ.
def get_smaller_primes(n):
smaller_primes = []
for num in range(2, n + 1):
if is_prime(num):
smaller_primes.append(num)
return smaller_primes
Но этот метод не оптимальный — его не стоит применять на практике. Есть более оптимальный метод - решето Эратосфена.
Алгоритм такой:
- Выписываем все целые числа от 0 до $n$. Сразу помечаем, что числа 0 и 1 не являются простыми (записываем на соответствующих этим числам позициях
False). - Заводим переменную $\mathrm{num}$, равную первому не рассмотренному простому числу. Изначально она равна 2.
- Помечаем в списке числа от $2 \cdot \mathrm{num}$ до $n$ с шагом, равным $\mathrm{num}$, составными. Например, для 2 пометим значением
cчётные числа — 4, 6, 8 и так далее. - Теперь в $\mathrm{num}$ присваиваем следующее простое число, то есть следующее не рассмотренное число в списке. Для этого достаточно увеличивать $\mathrm{num}$ с шагом 1, пропуская числа, отмеченные как составные. На первом найденном простом числе следует остановиться.
- Повторяем два предыдущих шага, пока это возможно. Код функции, реализующий решето Эратосфена:
def eratosthenes(n):
numbers = list(range(n + 1))
numbers[0] = numbers[1] = False
for num in range(2, n):
if numbers[num]:
for j in range(2 * num, n + 1, num):
numbers[j] = False
return numbers
eratosthenes(9)
[False, False, 2, 3, False, 5, False, 7, False, False]
Простые числа остались на своём месте. Там, где были составные числа, стоит False. Алгоритм можно оптимизировать. Для каждого простого числа pp начнём отмечать числа, начиная с $p^2$, как составные. Ведь все составные числа, которые меньше его, будут уже рассмотрены. Получится такой код:
def eratosthenes_effective(n):
numbers = list(range(n + 1))
numbers[0] = numbers[1] = False
for num in range(2, n):
if numbers[num]:
for j in range(num * num, n + 1, num):
numbers[j] = False
return numbers
Рассмотрим подробно пример работы алгоритма для $n = 15$.
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 # Запишем числа от 0 до 15
False False 2 3 4 5 6 7 8 9 10 11 12 13 14 15 # Отметим, что 0 и 1 не простые
num = 2 # Пометим все числа, кратные 2, начиная с 4, значением False
False False 2 3 False 5 False 7 False 9 False 11 False 13 False 15
num = 3 # Пометим все числа, кратные 3, начиная с 9, значением False
False False 2 3 False 5 False 7 False False False 11 False 13 False False
num = 5 # Алгоритм можно завершить, так как num**2 больше 15.
# Все числа, кратные 5 и меньшие 15, уже рассмотрены.
Решето Эратосфена работает за $O(n \log(\log n))$. Чтобы это доказать, нужно знать некоторые сложные факты из теории чисел.
Существует метод решения задачи нахождения всех простых чисел, не превосходящих $n$, которому требуется $O(n)$ операций. Он называется линейное решето. Этот метод помечает каждое число как составное только один раз.
Как и прежде, мы будем перебирать числа в порядке увеличения. Только в отличие от классического решета Эратосфена, составные числа не вычёркиваются. Вместо этого для каждого числа $x$ мы запишем наименьший простой делитель $p$. В программе мы будем записывать этот делитель в ячейку массива $\mathrm{lp}[x]$ (от англ. least prime). Если число простое, его наименьший простой делитель — оно само. Если число составное, его наименьший простой делитель $p$ уже встречался раньше. Более того, нам встречалось и число $i$, такое, что $x = i \cdot p$. На шаге $i$ мы должны пометить число $x$ как составное и указать его наименьший простой делитель. Каждое число будет помечено только один раз, на шаге $i = x/p$. Число $i$ может быть взято только одним способом, потому что у любого числа существует только один наименьший простой делитель $p$.
Алгоритм такой:
- Для каждого числа
iбудем хранитьlp[i]— минимальный простой делитель числаi. Заведём массивlpдлиныn + 1. А также массивprimes, в который будем добавлять найденные простые числа. - Перебираем
iпо возрастанию. - Если
lp[i] = 0, можно сделать вывод, что число i простое, и добавить его в массив primes. - Рассматриваем все простые числа p, которые не больше
lp[i]. Обновляемlp[p * i] = p.
def get_least_primes_linear(n):
lp = [0] * (n + 1)
primes = []
for i in range(2, n + 1):
if lp[i] == 0:
lp[i] = i
primes.append(i)
for p in primes:
x = p * i
if (p > lp[i]) or (x > n):
break
lp[x] = p
return primes, lp
get_least_primes_linear(8)
([2, 3, 5, 7], [0, 0, 2, 3, 2, 5, 2, 7, 2])
Основные структуры данных
Оперативная память и представление данных
Эффективность программы можно оценить по тому, как она расходует разные типы ресурсов компьютера. Основные из них — процессорное время и оперативная память. А ещё есть пропускная способность сетевых подключений, время работы жёсткого диска и некоторые другие ограниченные ресурсы.
На первом уроке мы говорили о том, как алгоритм использует процессорное время. Теперь нас будет интересовать потребление оперативной памяти — это называется пространственной сложностью алгоритма.
Как устроена оперативная память
Оперативная память, или ОЗУ — это своего рода «черновик», который программа использует для вычислений. В него можно записывать и перезаписывать информацию, и оттуда же её можно считывать.
Современные компьютеры располагают всего несколькими гигабайтами оперативной памяти, и данные исчезают из неё сразу после завершения работы программы. Поэтому эта память не подходит для длительного хранения информации, зато она работает в сотни раз быстрее SSD и во многие тысячи раз быстрее обыкновенного жёсткого диска.
Оперативная память разбита на ячейки размером в 1 байт. У каждой ячейки есть свой порядковый номер, который называется «адрес» (отдельные биты внутри ячейки адресов не имеют). Процессор взаимодействует с оперативной памятью напрямую и использует адреса, чтобы обращаться к данным, — почти как программа обращается к переменным по имени.
Чтобы понять, сколько памяти потребляет программа, нужно выяснить, сколько места занимают отдельные объекты. В разных языках программирования этот объём памяти может отличаться, но основные принципы будут общими. Для начала мы разберём, как используется память в языке C++, так как он позволяет сделать это очень эффективно, гибко и предсказуемо.
Представление базовых типов данных в ОП
Что можно записать в одну ячейку памяти? Как мы уже говорили, размер наименьшей ячейки — 1 байт, состоящий из 8 бит. Каждый бит может принимать одно из двух значений: либо 0, либо 1. Восемь бит позволяют закодировать всего $2^8=2562$ вариантов значений. Получается, что в такую ячейку можно записать, например, целое число в промежутке от 0 до 255.
Если считать эти числа номерами символов, то в 1 байт можно уместить 1 символ текста (тип char): все буквы латиницы и кириллицы, цифры и основные символы вполне умещаются в 256 вариантов.
Самый распространённый тип целых чисел int занимает 4 байта и позволяет закодировать числа от –2 147 483 648 до 2 147 483 647.
Эти границы можно вычислить: в 4 байтах содержится 32 бита. Один бит тратится на то, чтобы закодировать знак. Оставшийся 31 бит позволяет закодировать $2^{31} =2;147;483;6482$ чисел. Число «ноль» тоже нужно закодировать, поэтому положительных чисел остаётся на одно меньше, чем отрицательных.
Если ваши числа не превышают по модулю два миллиарда, можно пользоваться этим типом чисел. Обратите внимание, что всего чисел около четырёх миллиардов, но половина из них отрицательные. Если точно известно, что переменная не может быть отрицательной, можно воспользоваться типом беззнаковых целых unsigned int, он позволяет хранить числа от 0 до 4 294 967 295.
Вещественные (то есть дробные) числа чаще всего кодируются типом double — это «числа с плавающей точкой», которые занимают 8 байт. Они могут кодировать как очень большие числа, такие как $\pm10^{308}$, так и близкие к нулю, например $\pm10^{-308}$.
Составные типы данных
Теперь посчитаем, сколько памяти потребуется для хранения массива из 10 строк по 20 символов каждая.
Во-первых, потребуется хранить сам текст. Это займёт $$10; строк \cdot (20; \frac{символов}{строка}) \cdot (1;\frac{байт}{символ}) = 200; байт$$ Этого было бы достаточно, если бы строки располагались в памяти друг за другом. Но производить с ними какие-либо операции будет сложно.
Поэтому в массивы (и в другие составные структуры) зачастую помещаются не сами объекты, а только указатели на них — адреса, по которым они хранятся в ячейках оперативной памяти.
Во многих других языках каждый объект в программе записан в специальную «обёртку», которая, помимо данных, содержит вспомогательную информацию. Из-за этого, например, в языке Python даже короткие целые числа могут занимать не 4 байта, а почти 30 байт. Для хранения строки требуется около 40 байт вспомогательной информации, для хранения массива — ещё больше. Обычно объекты в таких языках ведут себя подобно строкам из предыдущего примера: они могут находиться в произвольном месте памяти, и любое обращение к ним происходит по сохранённому адресу.
Посчитаем, например, сколько памяти расходует массив из 10 чисел в Python и на что она уходит:
import sys
print(sys.getsizeof(42)) # => 28 байт занимает короткое целое число
print(sys.getsizeof([])) # => 56 байт занимает пустой массив
print(sys.getsizeof([42])) # => 64 = (56 + 8) байт занимает массив с одним элементом.
print(sys.getsizeof([1,2,3,5,6,7,8,9,10])) # => 136 = (56 + 8*10) байт занимает массив
# с десятью элементами.
# сами данные хранятся отдельно
# и добавляют 280 = (28 * 10) байт
Получается, мы тратим 56 байт на то, чтобы создать массив, а дальше по 8 байт на каждый новый объект в массиве — это адреса элементов. Но это ещё не всё. Ведь каждому числу нужно ещё по 28 байт. Итого массив из десяти чисел в Python занимает суммарно 56 + (8 + 28) * 10 байт = 416 байт. Сравните это с 40 байтами в языке C++.
Как освобождается память
Важно понимать, что если вы перестали пользоваться объектом, это ещё не значит, что он освободил занимаемую память. В языке C++ приходится следить за тем, чтобы выделенная память освобождалась. Встроенные контейнеры, такие как std::vector, упрощают задачу: они автоматически выделяют необходимую память при создании контейнера и освобождают её при выходе переменной контейнера из области видимости.
В большинстве других языков за освобождение памяти отвечает сборщик мусора, который время от времени проверяет, может ли объект ещё быть использован. Если оказывается, что на него больше не ссылается никакая переменная и никакой другой объект, то этот объект уничтожается.
Но сборка мусора — трудоёмкая операция, поэтому некоторые языки откладывают её до тех пор, пока свободное пространство не подойдёт к концу. Например, программы на Java (если их специально не ограничить при запуске) часто сталкиваются с проблемой высокого потребления памяти из-за хранения множества старых и уже неиспользуемых объектов.
Массивы постоянного размера
В предыдущих уроках мы говорили о том, как простые и составные типы данных могут храниться в оперативной памяти компьютера. Начиная с этого урока мы будем говорить о различных структурах данных. Структура данных — это способ организации информации в памяти, который позволяет проводить с ней определённый набор операций. Например, быстро искать или изменять данные.
Массив — одна из базовых структур данных. В этом уроке мы посмотрим, какие возможности бывают у разных типов массивов и как они могут быть реализованы.
Самый простой тип массивов имеет фиксированный размер и может хранить элементы одного и того же типа. Например, если мы создадим массив из десяти целых чисел, в него нельзя будет добавить ещё один элемент или записать объект неподходящего типа. Такие массивы вы можете встретить, например, в языке C — int numbers[10], или в С++ — std::array<int, 10> numbers.
С массивами фиксированного размера можно выполнить только две операции:
- узнать значение элемента по индексу,
- перезаписать значение по индексу.
Да, они не слишком функциональные, но зато очень эффективные. Каждая из операций выполняется за $O(1)$. Чтобы понять, как массиву удаётся настолько быстро находить нужный элемент, — разберёмся в его механике работы и посмотрим, как он хранит данные.
Как устроен массив
Массив — это набор однотипных данных, расположенных в памяти друг за другом. Поэтому он всегда занимает один непрерывный участок памяти. Точное местоположение этого участка операционная система сообщает программе в момент создания массива.
В начале выделенного участка памяти находится нулевой элемент, сразу за ним — первый и далее по порядку. Они идут друг за другом, без пропусков. Зная положение элемента в памяти — его адрес, мы можем этот элемент прочитать или записать. Теперь посмотрим, как узнать адрес элемента.
Пусть у нас есть массив numbers из 10 беззнаковых целых чисел. Адрес нулевого элемента нам известен — это 1000. Чтобы узнать положение следующего элемента, нам нужно прибавить к адресу начала размер элемента в байтах. Каждое число занимает по 4 байта, так что первый (нулевой) элемент займёт байты 1000, 1001, 1002, 1003. Значит, элемент с индексом 1 будет записан по адресу 1004.
Сложность вставки и удаления в динамических массивах
В прошлом уроке мы говорили о том, что такое массив и как он устроен. Теперь настало время познакомить вас с динамическими массивами. Иногда их ещё называют «векторами», потому что в C++ они реализуются классом std::vector. В Python динамические массивы реализуются классом list, но пусть вас не обманывает название — это не список, а именно массив.
Сложность вставки в динамический массив
Бывают ситуации, когда невозможно сказать точно, какая длина массива может понадобиться. Поэтому так важно иметь возможность добавлять элементы в массив прямо во время выполнения программы.
Нужно вставить элемент в произвольное место массива? Конечно, вставка в начало и в конец — частные случаи этой задачи. Вставка элемента в начало — худший случай. Сложность этой операции $O(n)$. Добавление элемента в конец — лучший случай. И его сложность $O(1)$.
Сложность удаления из динамического массива
При удалении, как и при вставке в массив, требуется сдвинуть все элементы правее ячейки, в которой происходит операция. При добавлении в массив элементы сдвигаются на один вправо. А при удалении — на один влево.
Реаллокация в динамических массивах
Массив нельзя просто расширить — ведь за его пределами в памяти уже записаны другие данные. При расширении массива они перезапишутся, что может привести к ошибке выполнения программы.
Поэтому, как правило, при расширении массива программе приходится произвести «реаллокацию» — выделить новый участок памяти и скопировать туда старое содержимое.
Выделение памяти — долгая операция, но копирование — это ещё большая проблема, ведь оно требует прохода по всем элементам, затратив $O(n)$ операций. Как же мы тогда можем утверждать, что добавление в конец массива стоит $O(1)$?
Напишем программу, которая добавляет в массив тысячу элементов — по одному за раз:
values = []
for i in range(1000):
values.append(i)
Операция append() может быть представлена как две операции: реаллокация и присваивание значения элементу массива. Для простоты мы не будем учитывать операции присваивания. Их число равно количеству добавляемых элементов; эта часть оптимизации не требует (и не может быть оптимизирована). А вот время, затрачиваемое на реаллокации, может существенно отличаться — в зависимости от выбранного подхода.
Если бы рассматриваемой программе приходилось при каждом добавлении элемента производить реаллокацию, итоговая сложность алгоритма была бы квадратичной. Теперь попробуем сократить число реаллокаций.
Во-первых, чтобы не приходилось на каждом шаге выделять дополнительную память, нужно держать запас свободного места в массиве. Например, если мы решим увеличить размер доступного массиву места сразу на 100 элементов, программа будет выделять память в 100 раз реже. Но программа всё ещё будет работать за $O(n^2)$, хотя и с небольшой константой при квадратичном члене.
Теперь у нас есть два разных размера массива: size (количество элементов) и capacity (ёмкость), причём size ≤ capacity.
Во-вторых, чтобы сделать сложность алгоритма линейной, нужно увеличивать размер не на фиксированное количество элементов (арифметическая прогрессия), а в фиксированное число раз (геометрическая прогрессия).
Пусть изначальная ёмкость массива равна 1, а при каждой реаллокации она удваивается. Тогда на первой реаллокации копируется 1 элемент, на второй — 2, на третьей — 4, затем — 8, 16, 32, 64, 128, 256, 512. После этих действий ёмкость массива равна 1024.
Посчитаем, сколько операций копирования нам нужно будет произвести к моменту добавления 1000-го элемента. Общее число копирований: $S = 1 + 2 + 4 + \cdots + 512 = 1024 - 1$.
В общем случае, если нужно добавить $n$ элементов (где $2^k \lt n \le 2^{k+1}$, последнее копирование затронет $2^k$ элементов. Напишем сумму такой геометрической прогрессии: $S = \sum_{i=0}^k 2^i = 2^{k+1} - 1 = 2 \cdot 2^k - 1 \le 2\cdot n$.
Итак, у нас получилось добиться того, что общее количество копирований при реаллокации будет линейно зависеть от числа элементов.
Связные списки
Как вы помните, элементы массива в памяти компьютера расположены последовательно. Чтобы вставить или удалить элемент из начала массива, нужно $O(n)$ операций. Потому что придётся передвинуть каждый последующий элемент.
Хорошо бы иметь структуру данных, в которой при вставке или удалении элемента передвигать остальные было бы не нужно.
Такая структура существует. Она называется «связный список» (англ. linked list). Во многих языках программирования реализована в стандартных типах, например, std::list в C++, LinkedList в Java.
Важно помнить, что в языке Python list — это динамический массив, хотя и обозначен словом «список».
Как устроен связный список
В связном списке у каждого элемента, помимо его значения, есть ссылка на следующий элемент списка. За исключением последнего — он ссылается в никуда. В зависимости от языка программирования ссылка в никуда может представлять собой объект None, нулевой указатель или аналогичную сущность. Кроме того, у связного списка принято определять точку старта — её называют «головой списка».
Достоинства и недостатки связного списка
Их элементы расположены в памяти компьютера в произвольных местах, а не по порядку, как в массиве. Это бывает очень удобно, если элементов много и расположить их единым блоком не представляется возможным.
Недостаток в том, что нельзя получить доступ к элементу за $O(1)$ по индексу, так как элементы хранятся в памяти непоследовательно. Для этого нужно пройти по всем элементам, начиная с головы списка, пока не дойдём до нужного. Это займёт $O(n)$ операций.
Двигаться по односвязному списку можно только в одном направлении. Из этого недостатка следует ещё один: мы не можем быстро удалить элемент, так как не знаем, какой элемент на него ссылается. В худшем случае потребуется $O(n)$ операций для поиска предыдущего. А вот вставить элемент после текущего мы можем быстро.
Структура данных стек
Структура данных стек часто встречается в программировании и во многих вещах, связанных с компьютерами. Стек работает по принципу LIFO.
Вы наверняка пользуетесь возможностью браузеров, реализованной с применением стека. Речь идёт о кнопке «назад». Нажмёте на неё один раз — вернётесь на предыдущую страницу, нажмёте снова — попадёте на страницу, где были до неё.
Во многих текстовых редакторах можно отменять последние операции. Эта функция тоже реализована при помощи стека.
Чтобы лучше понять, как устроен стек, представьте себе стопку книг в коробке. Если вам захочется почитать, вы сможете взять только верхнюю книгу. А если она окажется неинтересной, что ж, можно будет отбросить её и попытать удачу, взяв ещё одну книгу сверху, и так далее. Из стека также можно взять только верхний — последний, положенный в стек, — элемент.
Интерфейс стека
В отличие от массивов и связных списков, стек — это прежде всего удобный интерфейс для взаимодействия с данными, а не физическая особенность их хранения. Когда мы говорим про стек, мы подразумеваем структуру данных, которая реализует следующие методы:
push(item)— добавляет элемент на вершину стека;pop()— возвращает элемент с вершины стека и удаляет его;size()— возвращает размер стека (количество лежащих в нём элементов).
Иногда стек реализует дополнительные операции:
peek()илиtop()— возвращает элемент с вершины стека, не удаляя его;isEmpty()— определяет, пуст ли стек.
В большинстве случаев стек удобно реализовывать на массиве. Но бывают ситуации, когда стек должен хранить очень много элементов, а выделить единый блок памяти для этого невозможно. Тогда для реализации лучше воспользоваться связным списком.
Реализация стека
Посмотрите, как реализуется стек на основе массива. В конструкторе для экземпляра класса создаётся пустой массив. Далее при вызове методов push() и pop() этот массив будет меняться:
class Stack:
def __init__(self):
self.items = []
def push(self, item):
self.items.append(item)
def pop(self):
return self.items.pop()
def peek(self):
return self.items[-1]
def size(self):
return len(self.items)
stack = Stack()
stack.push('apple')
stack.push('banana')
stack.push('orange')
stack.pop()
Структуры данных: очередь и дек
В прошлом уроке вы познакомились со стеком и узнали, как он устроен. Ещё одна важная структура данных — «очередь». В отличие от стека, который работает по принципу LIFO, очередь основана на концепции FIFO. То есть первым извлекают элемент, который добавили раньше всех.
В повседневной жизни мы все сталкиваемся с очередями:
- Кассир в магазине обслуживает покупателей по одному: пока кто-то оплачивает свои продукты, остальным приходится стоять в очереди и ждать. И, конечно, вас обслужат не раньше, чем всех тех людей, которые встали в очередь до вашего прихода.
- Если мы звоним на горячую линию и все операторы заняты, нам тоже приходится ждать в очереди.
Подобные сценарии часто встречаются и в мире компьютеров. При их моделировании удобно применять структуру данных очередь.
Интерфейс очереди
Как и стек, очередь — интерфейс общения с данными. Он гарантирует наличие определённых методов, но не даёт никаких обещаний по способу хранения этих данных. То есть «под капотом» может находиться всё что угодно. При том, что интерфейс не накладывает ограничений на внутреннее устройство, очередь принято реализовывать таким образом, чтобы операции вставки и удаления элемента выполнялись за $O(1)$.
Когда мы говорим про очередь, мы ожидаем, что у структуры будут следующие методы:
push(item)— добавляет элемент в конец очереди;pop()— берёт элемент из начала очереди и удаляет его;peek()— берёт элемент из начала очереди без удаления;size()— возвращает количество элементов в очереди.
Стек вызовов
Код любой сложной программы разделён на множество функций. Поэтому работа всей системы описывается как взаимодействие небольших блоков кода. Базовые функции объединяются в сложные, а те — в ещё более сложные. В результате вся программа может быть представлена как одна сложносоставная функция, которая вызывает множество простых.
Как устроен стек вызовов
Допустим, мы написали программу на С++. Первой вызывается функция main(). В ней вызывается функция A. Она вызывает функцию B, которая, в свою очередь, вызывает C.
Так выглядит стек вызовов этой программы:

После возврата из функции управление должно вернуться туда, откуда эту функцию вызвали. Для этого при вызове функции в стеке вызовов сохраняется адрес той инструкции программы, которая будет выполнена после возврата из функции.
Для примера рассмотрим функцию, которая приветствует пользователя по имени и выдаёт ему гороскоп на сегодняшний день. Для простоты предположим, что пользователь пришёл на сайт, где всем выдают один и тот же гороскоп.
def say_hello(name):
print(f"Привет, {name}")
print_horoscope(name.upper())
print(f"Пока, {name}, хорошего дня!")
def print_horoscope(name):
print(f"{name}! Сегодня подходящий день для прогулок в парке и изучения рекурсии")
say_hello('Гоша')
Обратите внимание, что в разных частях программы переменная name может хранить разные значения. Например, при входе в функцию say_hello() в переменной name будет записано 'Гоша'. А если мы вызовем print_horoscope(), там появится 'ГОША'. Но, когда мы перейдём обратно в say_hello(), значение вновь вернётся к первоначальному 'Гоша'.
Чтобы добиться такого поведения, программа хранит все локальные переменные на том же стеке. Можно представить это так: на вершине стека находится структура, в которой записаны локальные переменные и аргументы функции, а также адрес возврата. Проследим, как меняется содержимое стека в нашем примере.
Работа стека: шаг за шагом
Первая команда, которая будет выполнена при старте программы, — вызов функции say_hello(). Под этот вызов на стеке выделяется блок памяти.

В выделенный блок памяти записывается адрес возврата. Он нужен для того, чтобы определить, куда передать управление после завершения работы функции. Как мы уже говорили, этот адрес соответствует инструкции, следующей сразу за местом вызова функции.
Также в стек помещаются переданные в функцию аргументы. С этих параметров начинается формирование набора локальных переменных функции. В нашем случае есть один аргумент name = 'Гоша', а другие локальные переменные отсутствуют.

Затем выполняется первая инструкция в функции say_hello(), которая выводит сообщение: «Привет, Гоша».
Далее происходит вызов метода upper(), который вернёт вызвавшей его функции строку 'ГОША', написанную большими буквами. Эта строка станет параметром функции print_horoscope().
Вызовы функции print() и метода upper() мы для краткости на картинке не показываем, хотя они, конечно же, тоже кладутся на стек при вызове и снимаются с него после завершения выполнения.
Когда вызывается функция print_horoscope() с параметром 'ГОША', под этот вызов выделяется новый блок памяти, куда записываются значения переданных функции параметров и новый адрес возврата, а также выделяется место для других локальных переменных. Блок памяти для функции print_horoscope() помещается поверх блока, отведённого под say_hello(). Помните стопку книг в коробке, о которой мы говорили пару уроков назад? Вот она, перед вами! Только вместо книг — блоки памяти.

Затем исполнится первая инструкция в функции print_horoscope(). Выведется сообщение: «ГОША! Сегодня подходящий день для прогулок в парке и изучения рекурсии!».
В print_horoscope() больше нет инструкций. Настал момент возвращения управления. В блоке памяти функции print_horoscope(), лежащем на стеке, записан адрес возврата, поэтому программе известно, какая инструкция должна исполниться следующей. Блок, отведённый под print_horoscope(), больше не нужен, и теперь извлекается из стека. Значение переменной name восстанавливается.

Затем исполняется инструкция из say_hello(), следующая за вызовом функции print_horoscope(). Эта инструкция — вывод сообщения: «Пока, Гоша, хорошего дня!»
Так как это последняя из инструкций в say_hello(), происходит возврат из функции. Блок памяти, выделенный под неё, освобождается.

Теперь вы знаете, как интерпретатор (или компилятор) языка программирования вызывает функции.
Рекурсия. Переполнение стека вызовов
В этом уроке мы поговорим о функциях, которые вызывают сами себя, но с изменёнными значениями аргументов. Такие функции называются «рекурсивными». И они тоже используют стек вызовов.
Факториал
Посмотрим на примере, в каких случаях могут понадобиться такие функции.
Факториал натурального числа можно вычислить как произведение всех натуральных чисел от 1 до n: $n! = 1 \cdot 2 \cdot ... \cdot (n-1) \cdot n$
Рекурсия и стек вызовов
Теперь напишем код рекурсивной функции вычисления факториала:
def factorial(n):
if n == 1 or n == 0:
return 1
return n * factorial(n - 1)
Проанализируем, что происходит при вызове функции factorial(3).

При каждом вызове функции на стеке создаётся новый набор локальных переменных. Таким образом, переменная n в каждом вызове оказывается новая. Благодаря этому переменные с одним и тем же именем даже в одной и той же функции не конфликтуют между собой. Невозможно обратиться к переменной n, которая относится к другому уровню рекурсии. Ни узнать, ни поменять её значение не получится.
Однако, чтобы хранить локальные переменные и адрес возврата на каждом уровне рекурсии, потребуется $O(d)$ памяти на стеке, где d — глубина рекурсии. При вычислении факториала $n!$ глубина рекурсии равна n, поэтому этот метод расходует $O(n)$ памяти на стеке.
А что будет, если эта память закончится, а рекурсивные вызовы продолжатся?
Стек вызовов переполнится и программа аварийно завершит работу.
Объём памяти, выделяемой под стек, ограничен очень небольшим объёмом — гораздо меньшим, чем общий объём оперативной памяти. Рекурсию нельзя делать больше, чем на несколько десятков тысяч вызовов в глубину, потому что при использовании слишком глубокой рекурсии стек переполнится (англ. stack overflow) и программа завершит работу аварийно с ошибкой. Программы на одних языках при этом выдадут исключение “Stack Overflow”, другие же завершатся с ошибкой “Segmentation Fault”.
factorial(10_000)
Что делать, чтобы стек не переполнялся
Есть несколько способов избежать переполнения стека:
- В некоторых случаях можно вовсе избавиться от рекурсии, заменив её на обыкновенный цикл. Например, вычисление факториала легко переписать следующим образом:
def factorial(n):
accumulator = 1
i = n
while i > 1:
accumulator *= i
i -= 1
return accumulator
- Другой способ заключается в том, чтобы написать свой собственный стек, эмулирующий стек вызовов, но лишённый ограничений встроенного.
Объёмом памяти, который выделяется под стек вызовов, можно управлять.
В некоторых языках это можно делать прямо в процессе работы программы. Например, в Python можно применить метод setrecursionlimit() модуля sys. Передаваемый в функцию параметр limit — задаёт максимальную глубину рекурсии. Наибольшее возможное значение зависит от платформы и всё равно существенно ограничено. Можно узнать текущее значение этой величины, вызвав метод getrecursionlimit().
В других языках программирования, таких как Java и JavaScript, размер стека вызовов можно задать настройками виртуальной машины при запуске программы, но в процессе работы программы он остаётся неизменным.
Кроме того, размер стека вызовов иногда может быть изменён на уровне операционной системы.
sys.getrecursionlimit()
Практика
Наивное решение. GET
@app.route('/', methods=['GET'])
def paginated_get():
page = int(request.args.get('page', '0'))
first = page * PAGE_SIZE
last = first + PAGE_SIZE
result = []
with open(FILE_PATH, 'r') as f:
for i, line in enumerate(f.readlines()[first:last]):
result.append( {'id': first + i, 'data': line.strip()})
return {"result": result}
Наивное решение. POST
@app.route('/', methods=['POST'])
def post():
data = request.json['data']
with open(FILE_PATH, 'a') as f:
f.write('\n' + data)
return {}, 201
Наивное решение. PUT
@app.route('/<int:data_id>', methods=['PUT'])
def put(data_id):
data = request.json['data']
with open(FILE_PATH, 'r') as f:
new_data = f.readlines()
new_data[data_id] = data + '\n'
with open(FILE_PATH, 'w') as f:
f.writelines(new_data)
return {}, 204
Наивное решение. DELETE
@app.route('/<int:data_id>', methods=['DELETE'])
def delete(data_id):
with open(FILE_PATH, 'r') as f:
new_data = f.readlines()
del new_data[data_id]
with open(FILE_PATH, 'w') as f:
f.writelines(new_data)
return {}, 204
Фиксированный. GET
@app.route('/', methods=['GET'])
def paginated_get():
page = int(request.args.get('page', '0'))
first = page * PAGE_SIZE
result = []
with open(FILE_PATH, 'rb') as f:
f.seek(first * ELEMENT_SIZE)
data = f.read(PAGE_SIZE * ELEMENT_SIZE)
for i, n in enumerate(range(PAGE_SIZE)):
result.append(
{
"id": first + i,
"data": (
data[n * ELEMENT_SIZE: (n + 1) * ELEMENT_SIZE].
strip(FILL_CHAR).decode('utf-8')
)
}
)
return {"result": result}
Фиксированный. POST
def post():
data = str(request.json['data'])
with open(FILE_PATH, 'a+b') as f:
f.write(data.encode('utf-8').ljust(ELEMENT_SIZE, FILL_CHAR))
return {}, 201
Фиксированный. PUT
@app.route('/<int:data_id>', methods=['PUT'])
def put(data_id):
data = request.json['data']
with open(FILE_PATH, 'r+b') as f:
f.seek(data_id * ELEMENT_SIZE)
f.write(data.encode('utf-8').ljust(ELEMENT_SIZE, FILL_CHAR))
return {}, 204
Фиксированный. DELETE
@app.route('/<int:data_id>', methods=['DELETE'])
def delete(data_id):
with open(FILE_PATH, 'r+b') as f:
point = data_id * ELEMENT_SIZE
f.seek(point)
while True:
f.seek(point + ELEMENT_SIZE)
complex_data = f.read(ELEMENT_SIZE)
f.seek(point)
if len(complex_data):
f.write(complex_data)
point += ELEMENT_SIZE
else:
f.truncate()
break
return {}, 204
Database. GET
@app.route('/', methods=['GET'])
def paginated_get():
page = int(request.args.get('page', '0'))
with closing(psycopg2.connect(dbname=dbname, host=host)) as conn:
with conn.cursor() as cursor:
cursor.execute(
'SELECT "id", "todo" FROM "todos" ORDER BY "id" OFFSET %s LIMIT %s;',
(page * PAGE_SIZE, (page + 1) * PAGE_SIZE)
)
return {
"result": [ {"id": row[0], "data": row[1]} for row in cursor]
}
Database. POST
@app.route('/', methods=['POST'])
def post():
data = str(request.json['data'])
with closing(psycopg2.connect(dbname=dbname, host=host)) as conn:
with conn.cursor() as cursor:
cursor.execute(
'INSERT INTO "todos" ("todo") VALUES (%s) RETURNING "id";',
(data,)
)
conn.commit()
return {"id": cursor.fetchone()[0]}, 201
Database. PUT
@app.route('/<int:data_id>', methods=['PUT'])
def put(data_id):
data = request.json['data']
with closing(psycopg2.connect(dbname=dbname, host=host)) as conn:
with conn.cursor() as cursor:
cursor.execute(
'UPDATE "todos" SET "todo" = %s WHERE "id" = %s;',
(data, data_id)
)
conn.commit()
return {}, 204
Database. DELETE
@app.route('/<int:data_id>', methods=['DELETE'])
def delete(data_id):
with closing(psycopg2.connect(dbname=dbname, host=host)) as conn:
with conn.cursor() as cursor:
cursor.execute(
'DELETE FROM "todos" WHERE "id" = %s;',
(data_id,)
)
conn.commit()
return {}, 204
Cache. GET
@app.route('/', methods=['GET'])
def paginated_get():
page = int(request.args.get('page', '0’))
redis_client = redis.StrictRedis(**redis_creds)
cached_page = redis_client.get(page)
if cached_page:
return cached_page
with closing(psycopg2.connect(**postgres_creds)) as conn:
with conn.cursor() as cursor:
cursor.execute(
'SELECT "id", "todo" FROM "todos" ORDER BY "id" OFFSET %s LIMIT %s;',
(page * PAGE_SIZE, (page + 1) * PAGE_SIZE)
)
result = json.dumps({
"result": [{"id": row[0], "data": row[1]} for row in cursor]
})
redis_client.set(page, result, ex=ttl)
return result
Рекурсия и сортировки
Введение. Примеры задач на рекурсию
Представь, что хочешь найти файл Kormen.pdf у себя в папке C:\books\. Как это сделать без использования автоматического поиска? Рассмотрим два варианта.
Вот схема первого варианта решения этой задачи:

Вот схема рекурсивного решения:

На каждом уровне погружения рекурсия добавляет блок в стек вызовов. Найдя нужный файл, функция останавливает рекурсию и начинает по цепочке — от одного уровня к другому — возвращать результат вызвавшей её программе.
Кстати, если говорить о скорости, то рекурсия не ускоряет работу программы, а наоборот, может её замедлить. Более того, алгоритмы, реализованные с применением циклов, часто исполняются быстрее. Зато рекурсия экономит время программиста, потому что код получается компактный и понятный, в нём труднее сделать ошибку. А ещё в такой код проще вносить изменения.
Рекурсивный и базовый случаи
Теперь мы расскажем о том, как правильно создавать рекурсию и что делать, если написанный вами рекурсивный алгоритм уходит в бесконечный цикл.
Любая корректно работающая рекурсия состоит из двух обязательных частей:
- рекурсивного случая, благодаря которому начинается прямой ход рекурсии и происходит её углубление;
- и базового случая, который в нужный момент останавливает это углубление и запускает обратный ход рекурсии.
Давайте поговорим о них подробнее.
Рекурсивный случай
функция stairs_builder(n):
построить 1 ступеньку
print("Осталось построить {n} ступеней.")
stairs_builder(n - 1)
Когда функция вызывает саму себя с изменёнными параметрами: stairs_builder(n - 1) — это и есть рекурсивный случай. И всё же, если мы запустим эту программу, компьютер зависнет.
Потому что наша рекурсия уйдёт в бесконечный цикл. На каждом следующем уровне рекурсии число ʜeпостроенных ступеней n уменьшается на 1. Но после n = 0 функция не остановит работу, а вызовется со значением −1, потом с −2 и так далее. Если бы у компьютера были неограниченные ресурсы, твоя лестница строилась бы вечно и имела бесконечное количество ступеней.
Базовый случай
При написании любой рекурсивной функции нужно указывать базовый случай — условие, при котором цепочка рекурсивных вызовов останавливается. При этом важно уметь определять, что именно должно происходить в базовом случае.
Чтобы функция stairs_builder() работала корректно, рекурсия должна остановиться в тот момент, когда будет построено нужное количество ступеней. То есть когда счётчик n = 0. Это и будет базовый случай!
функция stairs_builder(n):
if n == 0:
return
построить 1 ступеньку
print("Осталось построить {n} ступеней.")
stairs_builder(n - 1)
Как правильно создать рекурсию?
Чтобы решить задачу рекурсивным методом, нужно определить базовый и рекурсивный случаи.
Рекурсивный случай сводит задачу для большого набора данных к задаче с меньшим набором данных. Или для большого значения аргумента к задаче с меньшим значением аргумента.
А базовый случай определяет ситуацию, при которой рекурсию нужно остановить. Результат выполнения функции для базового случая следует вычислить явно, не прибегая к рекурсивным вызовам.
Ошибка, которую часто допускают, применяя рекурсию, — зацикливание. Обычно это происходит, если забыть указать базовый случай. Другая частая причина ухода в бесконечный цикл — это неверное изменение параметров в рекурсивном случае.
Например, если функция в какой-то ситуации вызывает саму себя, но значение параметра при этом не меняется. Тогда даже если базовый случай, который должен был бы прервать рекурсию, определён, функция может до него не дойти. При написании рекурсии мы должны убедиться, что для любого набора параметров функция рано или поздно сведётся к одному из базовых случаев.
В большинстве случаев программа, упавшая в кроличью нору бесконечной рекурсии, не будет работать вечно, а завершится с ошибкой переполнения стека вызовов или с ошибкой сегментации (англ. segmentation fault). Это происходит из-за ограниченности ресурсов компьютера, ведь каждый рекурсивный вызов расходует память на стеке.Как именно программа себя поведёт — зависит и от самого алгоритма, и от используемого компилятора. Подробнее об этом можно почитать в статье про оптимизацию хвостовой рекурсии (англ. tail call optimization).
Разбор задач. Рекурсивный перебор вариантов
Рекурсию часто применяют для генерации объектов. Например, числовых или скобочных последовательностей.
Генерация последовательностей из 0 и 1
Рассмотрим пример генерации всех возможных последовательностей длины n из нулей и единиц.
Функция принимает в качестве параметра число n и строку prefix. Вызываем функцию с параметром n и значением prefix, равным пустой строке. Далее будем добавлять в эту строку 0 и 1. В каждом рекурсивном вызове n означает, сколько ещё символов нужно добавить в строку. Рекурсия останавливается, когда n = 0, то есть символы добавлять больше не требуется. Это базовый случай рекурсии.
В рекурсивном случае функция вызывает себя дважды, но с разными параметрами. В первый раз она добавляет в строку prefix цифру 0, а во второй раз — 1. При этом значение n каждый раз уменьшается на 1, а prefix удлиняется на один символ. Таким образом, рекурсия уходит на n уровней в глубину.
Решение этой задачи удобно представлять в виде бинарного дерева. Начинаем с пустой строки. Если идём влево, добавляем 0, если вправо — 1. Если пройти от корня по всем веткам, получим все возможные последовательности из 0 и 1 длины 3.

Рекурсия часто используется для перебора вариантов. Например, у нас есть n различных предметов. Каждый из предметов может быть взят или отложен в сторону. Тогда есть $2^n$ вариантов того, как взять набор предметов. Пронумеруем предметы числами от 1 до $n$. Каждый предмет может быть взят (обозначим цифрой 1) или отложен в сторону (обозначим как 0). Так мы фактически свели задачу перебора вариантов к задаче генерации последовательностей из нулей и единиц.
def generate(n, prefix):
if n == 0:
print(prefix)
return
generate(n - 1, prefix + '0')
generate(n - 1, prefix + '1')
generate(3, '')
000
001
010
011
100
101
110
111
Алгоритмы сортировки. Знакомство
В прошлых уроках мы говорили о том, как с помощью рекурсии реализовывать двоичный поиск по отсортированному массиву, быстро возводить число в степень и перебирать всевозможные комбинации элементов. Теперь настало время познакомить вас с алгоритмами сортировок, с помощью которых можно наводить порядок в самых разных типах данных.
Сортировки среди нас
Упорядоченность данных очень важна в повседневной жизни.
Например, в вашем смартфоне контакты отсортированы по алфавиту. А расписание автобусов составляется по времени их отправления. Поисковая система выдаёт ранжированный список ответов — по степени их релевантности запросу.
Роль сортировок в решении задач
Во многих задачах работать с отсортированными данными удобнее, чем с неупорядоченными. Например:
- найти элемент в массиве быстрее чем за $O(n)$, воспользовавшись бинарным поиском, получится только на отсортированных данных;
- составить таблицу «10 лучших студентов курса» будет удобнее, если список студентов отсортирован не в алфавитном порядке, а по среднему баллу.
Нередко именно сортировка становится бутылочным горлышком и замедляет решение задачи. Поэтому важно знать, каким образом в каждом отдельном случае можно отсортировать массив наиболее эффективно.
Лучшей сортировки в общем случае не существует. Для разных типов входных данных и разных ограничений будет эффективнее использовать разные алгоритмы сортировки.
Выбор алгоритма сортировки
Рассмотрим два алгоритма сортировки:
- один работает быстро, но требует O(n)O(n) дополнительной памяти;
- другой алгоритм медленнее, но ему нужно лишь O(1)O(1) дополнительной памяти.
Например, сейчас в компании, старые сервера, на них совсем не осталось свободной памяти. На одном из них лежат все данные об удовлетворенности жизнью в разных городах страны. Для ежемесячного отчёта необходимо отсортировать данные и предоставить названия 100 городов с самыми довольными жителями. Отчёт надо сдать через неделю.
Лучше выбрать более медленный алгоритм, но эффективный по памяти.
Например, теперь команде поручили сделать стенд, на котором отображаются данные об удовлетворённости жителей страны в реальном времени. Под эту задачу был куплен новый мощный сервер. Каждую секунду на вход программы поступает обновлённый массив с текущими значениями индекса удовлетворённости по всем городам. Алгоритм должен составить «Топ-5 самых довольных городов» и обновлять этот список в режиме реального времени.
Лучше выбрать более быстрый алгоритм, но требующий больше памяти.
Таким образом, при решении задачи важно верно оценить имеющиеся ресурсы. В этом вам могут помочь следующие вопросы:
- Как быстро необходим ответ? Если результат сортировки нужен не срочно, то можно реализовать менее быстрый алгоритм, зато не использовать дополнительную память.
- С каким объёмом данных будет работать алгоритм? Если у вас в массиве всего 1000 элементов, то любой алгоритм сортировки упорядочит их так быстро, что вы и не заметите. Если же у вас в наличии 5 000 000 элементов, разница может быть уже существенной.
- Сколько памяти доступно? Если вам хватит свободного места на то, чтобы записать массив второй раз, можно упростить себе задачу и собирать отсортированный массив в дополнительной памяти, а не переставлять элементы в исходном массиве.
Устойчивость сортировок
Если после применения сортировки первоначальный порядок элементов с равным значением сравниваемого признака сохраняется, такая сортировка называется устойчивой (англ. stable sort). В противном случае, если элементы с равным значением поменялись местами, — неустойчивой.
Сортировка по ключу
Признак, по которому элементы сравниваются, называют «ключом сортировки». Мы уже сортировали элементы по ключу, когда нам требовалось упорядочить города по их индексу удовлетворённости.
Итак, с точки зрения алгоритма сортировки меняется только один этап — операция сравнения элементов.
Обычно функция сортировки принимает в качестве вспомогательного аргумента функцию, описывающую, в каком порядке идут элементы. Есть два распространённых способа это сделать:
- В одном варианте алгоритму сортировки передаётся в качестве параметра функция одного аргумента
key(object). Эта функция будет применена к каждому сравниваемому объекту, чтобы получить значение ключа для этого элемента. Все объекты попарно будут сравниваться между собой по этому ключу. - В другом варианте в алгоритм сортировки передаётся функция с двумя аргументами less(object_1, object_2), которая сравнивает два объекта и возвращает true, если первый объект должен быть расположен раньше второго, и false в противном случае. Такую функцию называют «компаратор» (англ. compare, «сравнивать»).
Сравнение элементов при помощи компаратора позволяет более гибко задавать порядок элементов, чем сравнение по ключу. Например, сортировку по любому ключу легко переписать в виде сортировки с таким компаратором:
функция less(object_1, object_2):
return key(object_1) < key(object_2)
А вот, например, сконструировать индекс по компаратору не всегда возможно. И, как мы ещё увидим, не все компараторы работают корректно. Поэтому обычно намного проще использовать функцию вычисления ключа сортировки.
Обязательно изучите документацию функции сортировки вашего любимого языка, чтобы научиться передавать в алгоритм сортировки компаратор либо функцию вычисления ключа.
Сортировка слиянием
Cортировка, которая работает всего за $O(n \log n)$. Она называется сортировка слиянием (англ. merge sort).
Принцип работы сортировки слиянием
Cоставные части алгоритма сортировки слиянием:
- Массив разбивается на две части примерно одинакового размера.
- Если в каком-то из получившихся подмассивов больше одного элемента, то для него рекурсивно запускается сортировка по этому же алгоритму, начиная с пункта 1.
- Два упорядоченных массива соединяются в один.
Условие остановки рекурсии — массив из одного элемента. Он не нуждается в сортировке, поэтому это базовый случай.

Дерево алгоритма сортировки слиянием: массив разбивается на части примерно равной длины. Каждая часть рекурсивно сортируется. После этого отсортированные части объединяются в единый массив
Сложность алгоритма
Сортировка слиянием даже в худшем случае работает за $O(n \log n)$. Давайте разберёмся почему.
На каждом шаге прямого хода рекурсии массив разбивается на две примерно равные по размеру части. Разбиение продолжается до тех пор, пока длина массива не станет равной 1. Таким образом, каждый элемент массива будет задействован примерно в $\log_2 n$ вызовах рекурсивной функции.
Иначе можно сказать, что глубина рекурсии составляет $O(\log_2n)$. Глубиной рекурсии называют максимальную глубину стека вызовов, которая достигается во время рекурсии.
На каждом шаге обратного хода рекурсии выполняется операция слияния двух отсортированных массивов. Как мы уже выяснили, для этого потребуется $O(n)$ операций, ведь на каждом уровне рекурсии нужно обработать $n$ чисел.
Таким образом, общая сложность этого алгоритма $O(n \cdot \log_2 n)$.
Пространственная сложность алгоритма
На каждом уровне рекурсии для проведения операций слияния требуется выделить $O(n)$ дополнительной памяти — в неё будут копироваться элементы объединяемых блоков в правильном порядке. Если выделять такое количество памяти на каждом уровне рекурсии, суммарно придётся затратить $O(n\log{n})$ дополнительной памяти.
Но вспомогательный массив требуется лишь временно. После объединения блоков мы можем перенести элементы из вспомогательного массива обратно в исходный, освободив выделенную память. Таким образом, в каждый момент времени будет использоваться вспомогательное пространство лишь для одного, текущего уровня рекурсии. Значит, нам будет достаточно использовать лишь $O(n)$ дополнительной памяти.
Устойчивость алгоритма
Сортировка слиянием является устойчивой сортировкой. В случае равенства элементов в двух отсортированных массивах, приоритет отдаётся элементу, который находился в левой половине массива. Так происходит на каждом уровне сортировки вплоть до объединения двух массивов длины в один. Таким образом, равные элементы в отсортированном массиве будут расположены друг относительно друга так же, как и в исходном.
Быстрая сортировка
В этом уроке мы рассмотрим ещё один популярный алгоритм сортировки, который называется быстрой сортировкой (англ. quick sort) и использует стратегию «разделяй и властвуй».
Встроенные функции сортировки во многих языках программирования используют модификации именно алгоритма быстрой сортировки, поскольку на практике она нередко работает даже быстрее сортировки слиянием. Автор этого алгоритма — Чарльз Хоар. Поэтому в честь него quick sort иногда называют сортировкой Хоара.
Принцип работы алгоритма
Алгоритм быстрой сортировки использует стратегию «разделяй и властвуй». Любой такой алгоритм состоит из трёх шагов:
- разделение данных на части меньшего размера;
- рекурсивный вызов алгоритма для этих частей;
- объединение результатов.
В алгоритме merge sort у нас был очень простой шаг разделения и нетривиальный шаг объединения данных. В алгоритме быстрой сортировки всё будет наоборот: мы сначала хитрым способом разделим данные на части, зато объединение произойдёт очень просто, нам достаточно будет дописать один отсортированный массив после другого.
- Возьмём исходный массив.

- Выберем какое-нибудь число. Все элементы, меньшие, чем это число, переложим в один массив. Все элементы, большие или равные этому числу, — в другой. Тогда элементы слева будут меньше элементов справа.

- Отсортируем каждую из частей рекурсивно.
- Склеим левую часть с правой.
Готово! Получился отсортированный массив:

У этого алгоритма очень простая идея. Но есть несколько моментов, которые в алгоритме придётся прояснить. Мы должны выбрать какое-нибудь число. А какое именно число мы выбираем?
Выбор опорного элемента
Если мы выберем слишком большое число, то мы получим очень несбалансированное разбиение. Например, если мы выберем максимальный элемент, то получим два пустых массива и один массив с одним элементом. В этом случае мы получим очень неэффективный алгоритм, который будет работать за $O(n^2)$. Поэтому мы должны выбирать опорный элемент так, чтобы получить сбалансированное разбиение. Например, можно выбирать средний элемент. Но это не всегда работает. Например, если массив отсортирован, то мы получим сбалансированное разбиение, но неэффективный алгоритм. Поэтому мы будем выбирать случайный элемент. Это позволит нам получить сбалансированное разбиение и эффективный алгоритм. Но в этом случае мы не сможем гарантировать, что алгоритм будет работать за $O(n log n)$. В худшем случае он будет работать за $O(n^2)$. Но в среднем он будет работать за $O(n log n)$.
Сложность быстрой сортировки
... и почему она нестабильна
Сортировка подсчётом
В начале спринта мы разобрали алгоритм, который в худшем случае имеет квадратичную сложность — сортировка вставками. Потом поговорили о быстрой сортировке, которая на практике работает быстрее и имеет сложность в среднем $O(n \log n)$, но в худшем случае работает за $O(n^2)$. А ещё разобрали сортировку слиянием, сложность которой даже в худшем случае — $O(n \log n)$.
Можно ли решить задачу сортировки быстрее чем за $O(n \log n)$? - Можно, но лишь для узкого класса задач.
Принцип работы алгоритма
Рассмотрим, как работает алгоритм сортировки подсчётом. Допустим, дан массив чисел:
nums = [5, 7, 1, 0, 1, 5, 11, 1]
Нужно отсортировать его по неубыванию. При этом мы знаем, что числа в нём обозначают номера месяцев. То есть значения в массиве находятся в диапазоне от 0 до 11.
Заведём массив из 12 элементов, заполненный нулями.
months = [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
Теперь пройдёмся по массиву nums и увеличим на 1 соответствующий элемент в массиве months:
months[5] += 1
months[7] += 1
months[1] += 1
months[0] += 1
months[1] += 1
months[5] += 1
months[11] += 1
months[1] += 1
Получим:
months = [1, 3, 0, 0, 0, 2, 0, 1, 0, 0, 0, 1]
Теперь пройдёмся по массиву months и добавим в массив nums столько элементов, сколько встречается в months:
nums = []
for i in range(len(months)):
for j in range(months[i]):
nums.append(i)
Получим:
nums = [0, 1, 1, 1, 5, 5, 7, 11]
Так работает алгоритм сортировки подсчётом. Закрепим знания кодом. Этот код будет работать, если значения элементов массива лежат в полуинтервале от 0 до k:
def counting_sort(nums, k):
# Создаём массив из k элементов, заполненный нулями
counts = [0] * k
# Проходим по массиву nums и увеличиваем соответствующий элемент в массиве counts
for num in nums:
counts[num] += 1
# Проходим по массиву counts и добавляем в массив nums столько элементов, сколько встречается в counts
nums = []
for i in range(len(counts)):
for j in range(counts[i]):
nums.append(i)
return nums
Алгоритм сортировки подсчётом использует $O(k)$ дополнительной памяти, где $k$ — мощность множества значений (количество различных значений, которые могут встретиться в массиве). Эта память используется для хранения вспомогательного массива. Чтобы создать вспомогательный массив, нужно знать диапазон возможных значений. В примере нам понадобился дополнительный массив всего из 12 элементов.
Хеш-функции
Что такое отображение
О массивах мы говорили в самом начале курса, и сейчас они нам очень пригодятся. Напомним, что в интерфейсе массива есть две основные операции:
get(index: int) -> value— получить значениеvalueиз ячейки с индексомindex;set(index: int, value: ValueType)— записать значениеvalueв ячейку с индексомindex.
Каждая из этих операций выполняется за $O(1)$. Это очень быстро! Однако у массивов есть одно серьёзное ограничение: хотя в ячейках массива можно расположить объекты любого типа, индексы этих ячеек могут быть исключительно целыми числами.
Но в программе часто возникает необходимость получить объект не по его порядковому номеру, то есть индексу ячейки в массиве, а по какому-то другому признаку, например по названию. Или, как говорят программисты, получить значение (англ. value) по ключу (англ. key).
Давайте представим, что у нас есть множество городов и множество стран. Одному городу может быть сопоставлена одна страна — та, в которой этот город находится.

Нужно написать такую программу-справочник, которая по городу будет узнавать страну, где тот расположен. А ещё нам пригодится функция добавления новой пары «город»: «страна», если справочник будет пополняться.
В этой задаче город является ключом, а страна — значением. Каждому городу сопоставлена ровно одна страна ни больше ни меньше. А вот на страну может указывать любое количество городов.
Такое сопоставление, когда каждому объекту первого множества (множество городов) соответствует ровно один объект второго множества (множество стран), называется «отображением» (англ. map).
На самом деле отображение — это другое название математического термина «функция», или «функциональная зависимость». Чаще всего функции отображают числа (расположенные на оси X) в другие числа (расположенные на оси Y). Для каждого числа из области определения функции можно выписать другое число — значение функции в этой точке.
Массивы — это тоже частный случай отображения: они умеют сопоставлять целому числу любое значение. Например, массив ["яблоко", "груша", "яблоко"] сопоставляет числам 0 и 2 строку яблоко, а числу 1 — строку груша.
Чтобы работать с отображениями, нам требуется похожая на массив структура данных, которая умеет получать и сохранять значения:
get(key: KeyType) -> value— получить значениеvalueпо ключуkey;set(key: KeyType, value: ValueType)— записать значениеvalueпо ключуkey.
Но вместо целочисленного индекса она должна допускать ключ произвольного типа.
Интерфейс, описывающий две этих операции, называют Map. А любую структуру, которая реализует этот интерфейс, называют «ассоциативным массивом» (англ. associative array).
Ассоциативные массивы
В большинстве языков программирования ассоциативные массивы встроены в язык.
Чаще всего их называют так же, как интерфейс — Map, «отображение», или используют производные от слова «хеш-таблица»: Hash, HashMap, HashTable и даже просто Table. Эти названия подчёркивают, каким именно способом был реализован интерфейс отображения. Встречаются и другие наименования. Например, в Python ассоциативные массивы называют «словарями» (англ. dictionary).
Есть два популярных способа реализовать или, как говорят программисты, имплементировать отображение. Первый способ, хеш-таблицы, мы рассмотрим в этом спринте. Другой способ основан на деревьях поиска. В некоторых языках встречаются сразу обе реализации. Например, в Java отображения имплементированы двумя отдельными классами: HashMap и TreeMap. В языке C++ им соответствуют классы std::unordered_map и std::map.
Ассоциативный массив — настолько полезная структура, что во многих языках есть встроенный синтаксис для её создания. К примеру, в Python отображение реализовано типом dict.
Наивная реализация ассоциативного массива
В этом спринте мы будем изучать универсальные и часто используемые ассоциативные массивы, а именно хеш-таблицы. Узнаем, как они устроены и как ими пользуются разработчики.
Но сначала давайте рассмотрим простейший способ реализации ассоциативного массива. Заведём обыкновенный массив или список, в котором записаны пары (key, value).
Если нужно получить элемент по ключу, достаточно пройти по всем элементам списка, выбрать пару с подходящим значением ключа и вернуть значение, записанное в этой паре. Если значение нужно записать, ищем пару с указанным ключом. Если находим, то изменяем её. А если такая пара не нашлась, создаём её и добавляем в конец массива.
структура Map:
pairs = []
метод get(key):
for pair in pairs:
if pair.key == key: # пара с указанным ключом найдена
return pair.value
return None
метод set(key, value):
for pair in pairs:
if pair.key == key: # пара с указанным ключом найдена
# обновить значение в найденной паре
pair.value = value
return
# пара с заданным ключом не найдена
добавить пару (key, value) в pairs
У нас получилась очень медленная реализация: на поиск элемента в таком массиве в среднем требуется $O(n)$ операций. В следующем уроке мы поговорим о том, как реализовать отображение более эффективным способом — при помощи хеш-таблиц.
Что такое хеш-таблица и хеш-функция
Хеш-таблица (англ. hash table) — это один из способов реализовать ассоциативный массив, при котором все данные записываются и хранятся в виде пар (key, value) в ячейках обыкновенного массива. Эти ячейки называются корзинами (англ. bucket). Как и в любом массиве, ячейки-корзины пронумерованы. Индекс, или номер корзины, в которую отправляются данные, зависит от ключа. Можно завести специальную функцию, которая по ключу будет вычислять номер корзины.
Как работают хеш-функция и хеш-таблица
Но как сделать такую функцию? Если у нас всего три ключа, мы можем написать несколько условных операторов, чтобы определить номер корзины. Но если ключей много, функция разрастётся и будет медленно работать.
Эта проблема решается с помощью специальной техники, которая называется «хеширование». Для этого нам понадобится хеш-функция.
Хеш-функция (англ. hash function) — функция, которая обеспечивает преобразование входных данных в целое число. Для разных типов объектов применяются разные хеш-функции. Результат вычисления хеш-функции называется «хешем» или «хеш-суммой» (англ. hash, hash code или digest).
Представим, что у каждой буквы алфавита есть свой индекс, равный её порядковому номеру. Хеш-функция может возвращать значение, равное индексу первой буквы в названии ключа. Тогда, например, для яблока функция вернёт 33, для груши — 4, а для сливы — 19.

Так как хеш — целое число, его можно использовать как номер корзины. Например, информация про груши хранится в корзине 4. Это значит, что когда нам нужно получить или обновить информацию про число груш, достаточно заглянуть в эту ячейку. При этом нам не требуется запоминать номера ячеек, ведь при помощи хеш-функции их всегда легко вычислить.

Другой пример хеш-функции: мы можем возвращать сумму всех номеров букв, входящих в название фрукта. Тогда для «яблоко» значение функции будет 92, для «груша» — 70, а для «слива» — 46.
Многие хеш-функции выдают огромные числа: миллионы, миллиарды, а иногда и ещё больше. Поэтому хеш редко используется напрямую как номер ячейки. Чаще всего хеш — это промежуточная стадия вычисления. Сначала по ключу мы определяем хеш, а затем по хешу — номер корзины.

Отображение из ключа в значение разделилось на три независимых отображения. 1. Сначала хеш-функция отображает ключ в число, то есть в хеш. 2. Затем этот хеш преобразуется в индекс корзины. 3. И, наконец, из массива корзин мы находим нужную корзину по её индексу. В ней-то и хранится значение, которое возвращается пользователю.
Что такое коллизии
Ситуация, когда хеш-функция для разных входных данных выдаёт одно и то же значение, называется «коллизией».
Например, и у «арбуза», и у «абрикоса» значение хеша будет равно 1. Получается, что оба ключа указывают на одну и ту же корзину хеш-таблицы.
Коллизии могут случаться у всех без исключения хеш-функций, поэтому в реализации хеш-таблицы обязательно должна быть заложена логика их разрешения.
Выбор размера хеш-таблицы и вычисление номера корзины
Вычисление номера корзины методом деления
Самый простой способ получить номер корзины $\mathrm{bucket}(k)$ для целого ключа $k$ — взять остаток от деления ключа $k$ на число корзин $M$. Остаток от деления обозначается $k \bmod M$ и произносится «$k$ по модулю $M$». В языках программирования остаток от деления вычисляется оператором %.
Любое целое число $k$ может быть представлено в форме $k = j\cdot M + r$, где все числа — целые, а $r \in[0,M)$. Число $r$ и называется остатком от деления.
Такое определение нам удобно, поскольку остатки от деления целого числа на $M$ могут принимать целые значения в диапазоне от $0$ до $(M-1)$, и это ровно те же числа, которые могут служить номерами корзин в хеш-таблице длины $M$.
Будьте аккуратны! В разных языках программирования остаток от деления по-разному работает с отрицательными числами (см. подробности). Не всегда это происходит так же, как математическая операция взятия по модулю. Например, выражение $-13 % 5$ в одних языках даст $2$, в других $-3$. Если не учесть эти нюансы, можно получить отрицательный номер корзины.
Выбор числа корзин
В качестве $M$ нужно брать простое число. То есть такое, которое делится без остатка только на себя и на 1.
Дело в том, что ключи могут быть неравномерно распределены не только в двоичной и десятичной системах счисления. Есть много других закономерностей, которым ключи могут подчиняться.
Чем больше делителей у $M$, тем чаще такие закономерности будут приводить к коллизиям. И наоборот, простое значение $M$ уменьшает число коллизий, ведь у простого числа всего два делителя.
Для любого числа корзин можно придумать такую киллер-последовательность из ключей, из-за которой случится много коллизий. Но если делителей у M много, велик шанс наткнуться на такую последовательность случайно. А когда M — большое простое число, это маловероятно.
Вычисление номера корзины методом умножения
Ещё один популярный способ, применяемый для вычисления номера ячейки — метод умножения. Для вычисления нам снова потребуется целое число. На этот раз мы его сразу обозначим буквой $h$, чтобы подчеркнуть, что это хеш ключа. Пусть количество корзин равно $M$. Также зададим константу $\alpha \in (0,1)$.
Тогда $\mathrm{bucket}(h) = \left [ M \cdot \left { h \cdot \alpha \right } \right ]$ , где $\left [ x \right ]$ — обозначает целую часть числа $x$, $\left { x \right }$ — его дробную часть.
Алгоритм построения хеш-функции с использованием метода умножения:
- Домножаем хеш ключа $h$ на выбранную константу $\alpha$.
- Берём от результата дробную часть. Получается некоторое значение из диапазона $[0,1)$. Важно, что эти значения для разных ключей будут равномерно рассеяны.
- Домножаем полученное значение на размер таблицы $M$. Числа получаются распределёнными в диапазоне $[0, M)$
- Берём от результата целую часть. С равными вероятностями получаются числа от $0$ до $(M−1)$ — это и будут номера корзин. Корзины будут заполняться равномерно, это поможет нам уменьшить число коллизий.
Дональд Кнут провёл исследования и выяснил, что хеш-функция получается хорошей, если в качестве $\alpha$ брать число, обратное золотому сечению. $$ \displaystyle \alpha = \phi^{-1} = \left ( \frac{\sqrt 5 -1}{2} \right ) = 0.6180339887... $$
Свойства хеш-функций
Не любая функция подходит на роль хеш-функции. Как мы выяснили, нам нужна такая функция, которая принимает на вход данные и выдаёт число, соответствующее индексу корзины. Чтобы сформулировать основные свойства хеш-функций, давайте вспомним, зачем эти функции нужны.
При работе с разными объектами нам важно быстро находить подходящее место для них в хеш-таблице. Благодаря быстрому вычислению хеш-функции ключа мы можем эффективно обновлять информацию об объектах: искать их, добавлять или удалять.
Например, пусть нам нужно выяснить стоимость товара в магазине. Если функция потратит на вычисление позиции элемента в таблице больше времени, чем мы затратим, если будем искать его последовательным перебором всех товаров, то смысла в применении такой функции нет.
Функция, преобразующая ключ в индекс корзины в хеш-таблице, должна обладать такими свойствами:
- Детерминизм. Для одного и того же ключа функция всегда должна возвращать одинаковое значение. Если в функции будет браться случайное значение, то повторное её применение может выдать новый индекс ячейки, а значит, мы не сможем получить искомые данные из хеш-таблицы. Хорошая функция при повторном вызове выполняет те же действия, что и при первичном. Например, взятие числа по модулю другого числа — детерминированная функция, так как результат всегда будет одинаковым.
- Эффективность. Хеш-функция должна вычисляться достаточно быстро. Сложность операции поиска в хеш-таблице складывается из сложности вычисления хеша и сложности поиска данных по хешу. Важно, чтобы оба процесса выполнялись эффективно.
- Ограниченность. Результат вычисления функции должен принадлежать определённому диапазону, который соответствует размеру хеш-таблицы. Поэтому обычно сначала вычисляют хеш-функцию, которая возвращает произвольное число. А потом этот результат берут по модулю $M$ (размер хеш-таблицы). Таким образом, любой ключ будет находиться в интервале от $0$ до $M-1$, а значит, мы никогда не обратимся к индексу, который не соответствует ни одной из корзин.
- Равномерность. Данные должны быть распределены по хеш-таблице равномерно. То есть каждое выходное значение — равновероятно. Равновероятно — это значит, что если мы запустим функцию для каждого элемента из большого списка разных объектов, то в результате получим примерно равное число ответов функции для каждого значения от $0$ до $M-1$. В противном случае в какие-то ячейки мы будем пытаться записать значение чаще, чем в другие. И это замедлит обращение к хеш-таблице. Пример неравномерной функции — получение среднесуточной температуры по городу и дате, так как большую часть времени температура держится на одном и том же уровне, а аномальные морозы или жара случаются редко.
Мы рассмотрели 4 свойства функции, которые важны при реализации хеш-таблиц. Но хеширование используется и в других задачах. Например, для хранения паролей, проверки неизменности файла в процессе передачи, шифрования сообщений при передаче по сети. Для этих задач выделяют ещё несколько свойств, которые могут быть полезны хеш-функциям.
- Лавинность. При незначительном изменении входных данных выходное значение должно меняться значительно. При хешировании паролей нелавинная функция проще взламывается. Если злоумышленник знает, что $h(aa) = 22$, а $h(bb) = 33$, то он может предположить такой $password$, что $h(password) = 44$. Перебрав небольшое число вариантов, злоумышленник сможет подобрать пароль по его хешу.
- Необратимость. Невозможно восстановить ключ по значению функции. Например, при регистрации на сайте пользователь вводит свой пароль, к которому применяется хеш-функция. Полученный хеш записывается в базу данных — в ячейку, соответствующую данному пользователю. Каждый раз, когда пользователь вводит пароль, к нему применяется та же функция. Так как алгоритм получения хеша от строки пароля в обоих случаях одинаковый, новый хеш совпадёт с записью в базе данных, если пользователь ввёл свой исходный пароль. Даже если злоумышленник получит доступ к данным в базе, у него не должно быть возможности восстановить пароль.
Построение хеш-функций для строк
Теперь давайте рассмотрим, как вычисляются хеш-функций для строк. Для этого есть специальный алгоритм, который называется «полиномиальным хешированием» (от слова «полином» — многочлен). Хеш строки $s$ вычисляется по формуле: $$ h(s)=\left(s_{1} q^{n-1}+s_{2} q^{n-2}+\cdots+s_{n-1} q+s_{n}\right) \bmod R $$ Где $s_i$ — код $i$-го символа (например, ASCII-код), $n$ — длина строки, а $R$ и $q$ — выбранные константы.
Все вычисления производятся по модулю некоторого большого числа $R$, поскольку для длинных строк сумма в скобках может оказаться слишком большой. В большинстве языков программирования при этом произойдёт переполнение типа целых чисел. В языках, где реализована так называемая «длинная арифметика», переполнения не случится, но с ростом значений складываемых и перемножаемых чисел вычисления будут становиться всё медленнее и медленнее.
Выбор числа $R$ зависит от типа переменной, в которой хранятся хеши. Например, для беззнаковых 4-байтовых целых чисел удобно выбрать $R=2^{32}$. Для 8-байтовых чисел можно взять $R=2^{64}$.
Если строки длинные, выбор величины $q$ не так важен — в сумму будут входить значения $q$ в достаточно больших степенях. Но ради универсальности лучше и в этом случае взять большое число. Число $q$ должно быть не только большим, но и простым.
Помните, мы говорили, что индекс корзины вычисляется взятием остатка от деления значения хеша на число корзин? Чем меньше общих делителей у $q$, $M$ и $R$, тем реже будут возникать коллизии. В качестве $R$ мы уже договорились использовать $2^{32}$, поэтому любое нечётное число не будет иметь с $R$ общих делителей.
Число $M$ будет меняться в зависимости от размера хеш-таблицы. При вычислении хеш-функции этот размер ещё не известен. Из-за этого мы не можем гарантировать, что параметр вычисления хеш-функции $q$ и число корзин $M$ будут взаимно простыми. Но выбор большого простого числа в качестве $q$ делает вероятность наличия нетривиальных общих делителей очень небольшой, ведь у простого числа нет делителей, кроме самого этого числа и единицы. Как мы говорили, $M$ обычно тоже делают простым, поэтому общие делители могут получиться, только когда $M=q$.
Поисковый индекс
Напомним основной принцип хеш-таблиц: если вы знаете, куда был положен элемент, то искать его нужно там же. Это правило часто применяют для быстрого поиска по данным.
Представьте, что вы пишете программу для чтения, и одной из её функций должен быть поиск по тексту. Пользователь вводит слово или строку, а программа находит и показывает их позиции в тексте.
Можно реализовать эту программу с помощью хеш-таблицы, в которой ключами будут строки, а значениями — массивы позиций, где эта строка встречается.
Отображение, которое каждому объекту ставит в соответствие его расположение, называют «поисковым индексом».
Если пользователь введёт любую подстроку, хеш-таблица должна найти её позиции. Значит, нужно предварительно добавить туда все возможные подстроки. А если подстроки в хеш-таблице не оказалось, получается, и в тексте её нет.
Этот способ позволит нам сразу получить нужную позицию — это, конечно, хорошо. Но он очень неэффективный. Ведь подстрок в тексте может быть столько, сколько существует способов выбрать две границы: $N\cdot(N-1)/ 2$, где $N$ — длина текста. Значит, в хеш-таблицу нужно добавить $O(N^2)$ пар (key, value). Поскольку ключами являются подстроки, каждая такая пара займёт в среднем $O(N)$ памяти. Получается, что всего при такой реализации придётся потратить $O(N^3)$ памяти.
Поэтому с большими текстами такая реализация не сработает.
...
Введение в вычислительную физику
Понятия сходимости, аппроксимации и устойчивости
Python Tutorial
Introduction
Python is a great general-purpose programming language on its own, but with the help of a few popular libraries (numpy, scipy, matplotlib and holoviews) it becomes a powerful environment for scientific computing.
We expect that many of you will have some experience with Python and Numpy; for the rest of you, this section will serve as a quick crash course both on the Python programming language and on the use of Python for scientific computing.
In this tutorial, we will cover:
- Basic Python: Basic data types, Functions, Classes
- Numpy: Arrays, Array indexing, Datatypes, Array math, Broadcasting
- Matplotlib: Plotting, Subplots, Images
- IPython: Creating notebooks, Typical workflows
Basics of Python
Python is a high-level, dynamically typed multiparadigm programming language. Python code is often said to be almost like pseudocode, since it allows you to express very powerful ideas in very few lines of code while being very readable.
We recommend to read PEP 8.
Python versions and Zen of Python
There are currently supported versions of Python 3.X. Support for Python 2.7 ended in 2020. For this class all code will use Python 3.7.
You can check your Python version at the command line by running python --version.
!python --version
Python 3.7.4
import this
The Zen of Python, by Tim Peters
Beautiful is better than ugly.
Explicit is better than implicit.
Simple is better than complex.
Complex is better than complicated.
Flat is better than nested.
Sparse is better than dense.
Readability counts.
Special cases aren't special enough to break the rules.
Although practicality beats purity.
Errors should never pass silently.
Unless explicitly silenced.
In the face of ambiguity, refuse the temptation to guess.
There should be one-- and preferably only one --obvious way to do it.
Although that way may not be obvious at first unless you're Dutch.
Now is better than never.
Although never is often better than *right* now.
If the implementation is hard to explain, it's a bad idea.
If the implementation is easy to explain, it may be a good idea.
Namespaces are one honking great idea -- let's do more of those!
Basic data types
Numbers
Integers and floats work as you would expect from other languages:
x = 3
print(x, type(x))
3 <class 'int'>
print(x + 1) # Addition;
print(x - 1) # Subtraction;
print(x * 2) # Multiplication;
print(x ** 2) # Exponentiation;
4
2
6
9
x += 1
print(x) # Prints "4"
x *= 2
print(x) # Prints "8"
4
8
y = 2.5
print(type(y)) # Prints "<type 'float'>"
print(y, y + 1, y * 2, y ** 2) # Prints "2.5 3.5 5.0 6.25"
<class 'float'>
2.5 3.5 5.0 6.25
Note that unlike many languages, Python does not have unary increment (x++) or decrement (x--) operators.
Python also has built-in types for long integers and complex numbers; you can find all of the details in the documentation.
Booleans
Python implements all of the usual operators for Boolean logic, but uses English words rather than symbols (&&, ||, etc.):
T, F = True, False
print(type(T)) # Prints "<type 'bool'>"
<class 'bool'>
Now we let's look at the operations:
print(T and F) # Logical AND;
print(T or F) # Logical OR;
print(not T) # Logical NOT;
print(T != F) # Logical XOR;
False
True
False
True
Strings
hello = 'hello' # String literals can use single quotes
world = "world" # or double quotes; it does not matter.
print(hello, len(hello))
hello 5
hw = hello + ' ' + world # String concatenation
print(hw) # prints "hello world"
hello world
hw12 = '%s %s %d' % (hello, world, 12) # sprintf style string formatting
print(hw12) # prints "hello world 12"
hello world 12
String objects have a bunch of useful methods; for example:
s = "hello"
print(s.capitalize()) # Capitalize a string; prints "Hello"
print(s.upper()) # Convert a string to uppercase; prints "HELLO"
print(s.rjust(7)) # Right-justify a string, padding with spaces; prints " hello"
print(s.center(7)) # Center a string, padding with spaces; prints " hello "
print(s.replace('l', '(ell)')) # Replace all instances of one substring with another;
# prints "he(ell)(ell)o"
print(' world '.strip()) # Strip leading and trailing whitespace; prints "world"
Hello
HELLO
hello
hello
he(ell)(ell)o
world
You can find a list of all string methods in the documentation.
Containers
Python includes several built-in container types: lists, dictionaries, sets, and tuples.
Lists
A list is the Python equivalent of an array, but is resizeable and can contain elements of different types:
xs = [3, 1, 2] # Create a list
print(xs, xs[2])
print(xs[-1]) # Negative indices count from the end of the list; prints "2"
[3, 1, 2] 2
2
xs[2] = 'foo' # Lists can contain elements of different types
print(xs)
[3, 1, 'foo']
xs.append('bar') # Add a new element to the end of the list
print(xs)
[3, 1, 'foo', 'bar']
x = xs.pop() # Remove and return the last element of the list
print(x, xs)
bar [3, 1, 'foo']
As usual, you can find all the gory details about lists in the documentation.
Slicing
In addition to accessing list elements one at a time, Python provides concise syntax to access sublists; this is known as slicing:
nums = range(5) # range is a built-in function that creates a list of integers
print(nums) # Prints "[0, 1, 2, 3, 4]"
print(nums[2:4]) # Get a slice from index 2 to 4 (exclusive); prints "[2, 3]"
print(nums[2:]) # Get a slice from index 2 to the end; prints "[2, 3, 4]"
print(nums[:2]) # Get a slice from the start to index 2 (exclusive); prints "[0, 1]"
print(nums[:]) # Get a slice of the whole list; prints ["0, 1, 2, 3, 4]"
print(nums[:-1]) # Slice indices can be negative; prints ["0, 1, 2, 3]"
range(0, 5)
range(2, 4)
range(2, 5)
range(0, 2)
range(0, 5)
range(0, 4)
Loops
You can loop over the elements of a list like this:
animals = ['cat', 'dog', 'monkey']
for animal in animals:
print(animal)
cat
dog
monkey
If you want access to the index of each element within the body of a loop, use the built-in enumerate function:
animals = ['cat', 'dog', 'monkey']
for idx, animal in enumerate(animals):
print('#%d: %s' % (idx + 1, animal))
#1: cat
#2: dog
#3: monkey
List comprehensions:
When programming, frequently we want to transform one type of data into another. As a simple example, consider the following code that computes square numbers:
nums = [0, 1, 2, 3, 4]
squares = []
for x in nums:
squares.append(x ** 2)
print(squares)
[0, 1, 4, 9, 16]
You can make this code simpler using a list comprehension:
nums = [0, 1, 2, 3, 4]
squares = [x ** 2 for x in nums]
print(squares)
[0, 1, 4, 9, 16]
List comprehensions can also contain conditions:
nums = [0, 1, 2, 3, 4]
even_squares = [x ** 2 for x in nums if x % 2 == 0]
print(even_squares)
[0, 4, 16]
Dictionaries
A dictionary stores (key, value) pairs, similar to a Map in Java or an object in Javascript. You can use it like this:
d = {'cat': 'cute', 'dog': 'furry'} # Create a new dictionary with some data
print(d['cat']) # Get an entry from a dictionary; prints "cute"
print('cat' in d) # Check if a dictionary has a given key; prints "True"
cute
True
d['fish'] = 'wet' # Set an entry in a dictionary
print(d['fish']) # Prints "wet"
wet
print(d.get('monkey', 'N/A')) # Get an element with a default; prints "N/A"
print(d.get('fish', 'N/A')) # Get an element with a default; prints "wet"
N/A
wet
del d['fish'] # Remove an element from a dictionary
print(d.get('fish', 'N/A')) # "fish" is no longer a key; prints "N/A"
N/A
You can find all you need to know about dictionaries in the documentation.
It is easy to iterate over the keys in a dictionary:
d = {'person': 2, 'cat': 4, 'spider': 8}
for animal in d:
legs = d[animal]
print('A %s has %d legs' % (animal, legs))
A person has 2 legs
A cat has 4 legs
A spider has 8 legs
Dictionary comprehensions: These are similar to list comprehensions, but allow you to easily construct dictionaries. For example:
nums = [0, 1, 2, 3, 4]
even_num_to_square = {x: x ** 2 for x in nums if x % 2 == 0}
print(even_num_to_square)
{0: 0, 2: 4, 4: 16}
Sets
A set is an unordered collection of distinct elements. As a simple example, consider the following:
animals = {'cat', 'dog'}
print('cat' in animals) # Check if an element is in a set; prints "True"
print('fish' in animals) # prints "False"
True
False
animals.add('fish') # Add an element to a set
print('fish' in animals)
print(len(animals)) # Number of elements in a set;
True
3
animals.add('cat') # Adding an element that is already in the set does nothing
print(len(animals))
animals.remove('cat') # Remove an element from a set
print(len(animals))
3
2
Loops: Iterating over a set has the same syntax as iterating over a list; however since sets are unordered, you cannot make assumptions about the order in which you visit the elements of the set:
animals = {'cat', 'dog', 'fish'}
for idx, animal in enumerate(animals):
print('#%d: %s' % (idx + 1, animal))
# Prints "#1: fish", "#2: dog", "#3: cat"
#1: fish
#2: dog
#3: cat
Set comprehensions: Like lists and dictionaries, we can easily construct sets using set comprehensions:
from math import sqrt
print({int(sqrt(x)) for x in range(30)})
{0, 1, 2, 3, 4, 5}
Tuples
A tuple is an (immutable) ordered list of values. A tuple is in many ways similar to a list; one of the most important differences is that tuples can be used as keys in dictionaries and as elements of sets, while lists cannot. Here is a trivial example:
d = {(x, x + 1): x for x in range(10)} # Create a dictionary with tuple keys
t = (5, 6) # Create a tuple
print(type(t))
print(d[t])
print(d[(1, 2)])
<class 'tuple'>
5
1
Functions
Python functions are defined using the def keyword. For example:
def sign(x: float) -> str:
'''Function sign''' # document line
if x > 0:
return 'positive'
elif x < 0:
return 'negative'
else:
return 'zero'
for x in [-1, 0, 1]:
print(sign(x))
negative
zero
positive
help(sign)
Help on function sign in module __main__:
sign(x: float) -> str
Function sign
We will often define functions to take optional keyword arguments, like this:
def hello(name: str, loud: bool=False) -> None:
'''Function hello
If loud is True,
then the name is printed in capital letters.
'''
if loud:
print('HELLO, %s' % name.upper())
else:
print('Hello, %s!' % name)
hello('Bob')
hello('Fred', loud=True)
Hello, Bob!
HELLO, FRED
help(hello)
Help on function hello in module __main__:
hello(name: str, loud: bool = False) -> None
Function hello
If loud is True,
then the name is printed in capital letters.
Classes
The syntax for defining classes in Python is straightforward:
class Greeter:
'''Class Greeter
method greet:
If loud is True,
then the name is printed in capital letters.
'''
# Constructor
def __init__(self, name):
self.name = name # Create an instance variable
# Instance method
def greet(self, loud: bool=False) ->None:
if loud:
print('HELLO, %s!' % self.name.upper())
else:
print('Hello, %s' % self.name)
g = Greeter('Fred') # Construct an instance of the Greeter class
g.greet() # Call an instance method; prints "Hello, Fred"
g.greet(loud=True) # Call an instance method; prints "HELLO, FRED!"
Hello, Fred
HELLO, FRED!
help(Greeter)
Help on class Greeter in module __main__:
class Greeter(builtins.object)
| Greeter(name)
|
| Class Greeter
|
| method greet:
| If loud is True,
| then the name is printed in capital letters.
|
| Methods defined here:
|
| __init__(self, name)
| Initialize self. See help(type(self)) for accurate signature.
|
| greet(self, loud: bool = False) -> None
| # Instance method
|
| ----------------------------------------------------------------------
| Data descriptors defined here:
|
| __dict__
| dictionary for instance variables (if defined)
|
| __weakref__
| list of weak references to the object (if defined)
Numpy
Numpy is the core library for scientific computing in Python. It provides a high-performance multidimensional array object, and tools for working with these arrays.
To use Numpy, we first need to import the numpy package:
import numpy as np
Arrays
A numpy array is a grid of values, all of the same type, and is indexed by a tuple of nonnegative integers. The number of dimensions is the rank of the array; the shape of an array is a tuple of integers giving the size of the array along each dimension.
We can initialize numpy arrays from nested Python lists, and access elements using square brackets:
a = np.array([1, 2, 3]) # Create a rank 1 array
print(type(a), a.shape, a[0], a[1], a[2])
a[0] = 5 # Change an element of the array
print(a)
<class 'numpy.ndarray'> (3,) 1 2 3
[5 2 3]
b = np.array([[1,2,3],[4,5,6]]) # Create a rank 2 array
print(b)
[[1 2 3]
[4 5 6]]
print(b.shape)
print(b[0, 0], b[0, 1], b[1, 0])
(2, 3)
1 2 4
Numpy also provides many functions to create arrays:
a = np.zeros((2,2)) # Create an array of all zeros
print(a)
[[0. 0.]
[0. 0.]]
b = np.ones((1,2)) # Create an array of all ones
print(b)
[[1. 1.]]
c = np.full((2,2), 7) # Create a constant array
print(c)
[[7 7]
[7 7]]
d = np.eye(2) # Create a 2x2 identity matrix
print(d)
[[1. 0.]
[0. 1.]]
e = np.random.random((2,2)) # Create an array filled with random values
print(e)
[[0.57584699 0.0757792 ]
[0.18793454 0.78004389]]
Array indexing
Numpy offers several ways to index into arrays.
Slicing: Similar to Python lists, numpy arrays can be sliced. Since arrays may be multidimensional, you must specify a slice for each dimension of the array:
import numpy as np
# Create the following rank 2 array with shape (3, 4)
# [[ 1 2 3 4]
# [ 5 6 7 8]
# [ 9 10 11 12]]
a = np.array([[1,2,3,4], [5,6,7,8], [9,10,11,12]])
# Use slicing to pull out the subarray consisting of the first 2 rows
# and columns 1 and 2; b is the following array of shape (2, 2):
# [[2 3]
# [6 7]]
b = a[:2, 1:3]
print(b)
[[2 3]
[6 7]]
A slice of an array is a view into the same data, so modifying it will modify the original array.
print(a[0, 1])
b[0, 0] = 77 # b[0, 0] is the same piece of data as a[0, 1]
print(a[0, 1])
2
77
You can also mix integer indexing with slice indexing. However, doing so will yield an array of lower rank than the original array.
# Create the following rank 2 array with shape (3, 4)
a = np.array([[1,2,3,4], [5,6,7,8], [9,10,11,12]])
print(a)
[[ 1 2 3 4]
[ 5 6 7 8]
[ 9 10 11 12]]
Two ways of accessing the data in the middle row of the array. Mixing integer indexing with slices yields an array of lower rank, while using only slices yields an array of the same rank as the original array:
row_r1 = a[1, :] # Rank 1 view of the second row of a
row_r2 = a[1:2, :] # Rank 2 view of the second row of a
row_r3 = a[[1], :] # Rank 2 view of the second row of a
print(row_r1, row_r1.shape)
print(row_r2, row_r2.shape)
print(row_r3, row_r3.shape)
[5 6 7 8] (4,)
[[5 6 7 8]] (1, 4)
[[5 6 7 8]] (1, 4)
# We can make the same distinction when accessing columns of an array:
col_r1 = a[:, 1]
col_r2 = a[:, 1:2]
print(col_r1, col_r1.shape)
print(col_r2, col_r2.shape)
[ 2 6 10] (3,)
[[ 2]
[ 6]
[10]] (3, 1)
Integer array indexing: When you index into numpy arrays using slicing, the resulting array view will always be a subarray of the original array. In contrast, integer array indexing allows you to construct arbitrary arrays using the data from another array. Here is an example:
a = np.array([[1,2], [3, 4], [5, 6]])
# An example of integer array indexing.
# The returned array will have shape (3,) and
print(a[[0, 1, 2], [0, 1, 0]])
# The above example of integer array indexing is equivalent to this:
print(np.array([a[0, 0], a[1, 1], a[2, 0]]))
[1 4 5]
[1 4 5]
# When using integer array indexing, you can reuse the same
# element from the source array:
print(a[[0, 0], [1, 1]])
# Equivalent to the previous integer array indexing example
print(np.array([a[0, 1], a[0, 1]]))
[2 2]
[2 2]
One useful trick with integer array indexing is selecting or mutating one element from each row of a matrix:
# Create a new array from which we will select elements
a = np.array([[1,2,3], [4,5,6], [7,8,9], [10, 11, 12]])
print(a)
[[ 1 2 3]
[ 4 5 6]
[ 7 8 9]
[10 11 12]]
# Create an array of indices
b = np.array([0, 2, 0, 1])
# Select one element from each row of a using the indices in b
print(a[np.arange(4), b]) # Prints "[ 1 6 7 11]"
[ 1 6 7 11]
# Mutate one element from each row of a using the indices in b
a[np.arange(4), b] += 10
print(a)
[[11 2 3]
[ 4 5 16]
[17 8 9]
[10 21 12]]
Boolean array indexing: Boolean array indexing lets you pick out arbitrary elements of an array. Frequently this type of indexing is used to select the elements of an array that satisfy some condition. Here is an example:
import numpy as np
a = np.array([[1,2], [3, 4], [5, 6]])
bool_idx = (a > 2) # Find the elements of a that are bigger than 2;
# this returns a numpy array of Booleans of the same
# shape as a, where each slot of bool_idx tells
# whether that element of a is > 2.
print(bool_idx)
[[False False]
[ True True]
[ True True]]
# We use boolean array indexing to construct a rank 1 array
# consisting of the elements of a corresponding to the True values
# of bool_idx
print(a[bool_idx])
# We can do all of the above in a single concise statement:
print(a[a > 2])
[3 4 5 6]
[3 4 5 6]
For brevity we have left out a lot of details about numpy array indexing; if you want to know more you should read the documentation.
Datatypes
Every numpy array is a grid of elements of the same type. Numpy provides a large set of numeric datatypes that you can use to construct arrays. Numpy tries to guess a datatype when you create an array, but functions that construct arrays usually also include an optional argument to explicitly specify the datatype. Here is an example:
x = np.array([1, 2]) # Let numpy choose the datatype
y = np.array([1.0, 2.0]) # Let numpy choose the datatype
z = np.array([1, 2], dtype=np.int64) # Force a particular datatype
print(x.dtype, y.dtype, z.dtype)
int64 float64 int64
You can read all about numpy datatypes in the documentation.
Array math
Basic mathematical functions operate elementwise on arrays, and are available both as operator overloads and as functions in the numpy module:
x = np.array([[1,2],[3,4]], dtype=np.float64)
y = np.array([[5,6],[7,8]], dtype=np.float64)
# Elementwise sum; both produce the array
print(x + y)
print(np.add(x, y))
[[ 6. 8.]
[10. 12.]]
[[ 6. 8.]
[10. 12.]]
# Elementwise difference; both produce the array
print(x - y)
print(np.subtract(x, y))
[[-4. -4.]
[-4. -4.]]
[[-4. -4.]
[-4. -4.]]
# Elementwise product; both produce the array
print(x * y)
print(np.multiply(x, y))
[[ 5. 12.]
[21. 32.]]
[[ 5. 12.]
[21. 32.]]
# Elementwise division; both produce the array
# [[ 0.2 0.33333333]
# [ 0.42857143 0.5 ]]
print(x / y)
print(np.divide(x, y))
[[0.2 0.33333333]
[0.42857143 0.5 ]]
[[0.2 0.33333333]
[0.42857143 0.5 ]]
# Elementwise square root; produces the array
# [[ 1. 1.41421356]
# [ 1.73205081 2. ]]
print(np.sqrt(x))
[[1. 1.41421356]
[1.73205081 2. ]]
Note that unlike MATLAB, * is elementwise multiplication, not matrix multiplication. We instead use the dot function to compute inner products of vectors, to multiply a vector by a matrix, and to multiply matrices. dot is available both as a function in the numpy module and as an instance method of array objects:
x = np.array([[1,2],[3,4]])
y = np.array([[5,6],[7,8]])
v = np.array([9,10])
w = np.array([11, 12])
# Inner product of vectors; both produce 219
print(v.dot(w))
print(np.dot(v, w))
219
219
# Matrix / vector product; both produce the rank 1 array [29 67]
print(x.dot(v))
print(np.dot(x, v))
[29 67]
[29 67]
# Matrix / matrix product; both produce the rank 2 array
# [[19 22]
# [43 50]]
print(x.dot(y))
print(np.dot(x, y))
[[19 22]
[43 50]]
[[19 22]
[43 50]]
Numpy provides many useful functions for performing computations on arrays; one of the most useful is sum:
x = np.array([[1,2],[3,4]])
print(np.sum(x)) # Compute sum of all elements; prints "10"
print(np.sum(x, axis=0)) # Compute sum of each column; prints "[4 6]"
print(np.sum(x, axis=1)) # Compute sum of each row; prints "[3 7]"
10
[4 6]
[3 7]
You can find the full list of mathematical functions provided by numpy in the documentation.
Apart from computing mathematical functions using arrays, we frequently need to reshape or otherwise manipulate data in arrays. The simplest example of this type of operation is transposing a matrix; to transpose a matrix, simply use the T attribute of an array object:
print(x)
print(x.T)
[[1 2]
[3 4]]
[[1 3]
[2 4]]
v = np.array([[1,2,3]])
print(v)
print(v.T)
[[1 2 3]]
[[1]
[2]
[3]]
Broadcasting
Broadcasting is a powerful mechanism that allows numpy to work with arrays of different shapes when performing arithmetic operations. Frequently we have a smaller array and a larger array, and we want to use the smaller array multiple times to perform some operation on the larger array.
For example, suppose that we want to add a constant vector to each row of a matrix. We could do it like this:
# We will add the vector v to each row of the matrix x,
# storing the result in the matrix y
x = np.array([[1,2,3], [4,5,6], [7,8,9], [10, 11, 12]])
v = np.array([1, 0, 1])
y = np.empty_like(x) # Create an empty matrix with the same shape as x
# Add the vector v to each row of the matrix x with an explicit loop
for i in range(4):
y[i, :] = x[i, :] + v
print(y)
[[ 2 2 4]
[ 5 5 7]
[ 8 8 10]
[11 11 13]]
This works; however when the matrix x is very large, computing an explicit loop in Python could be slow. Note that adding the vector v to each row of the matrix x is equivalent to forming a matrix vv by stacking multiple copies of v vertically, then performing elementwise summation of x and vv. We could implement this approach like this:
vv = np.tile(v, (4, 1)) # Stack 4 copies of v on top of each other
print(vv) # Prints "[[1 0 1]
# [1 0 1]
# [1 0 1]
# [1 0 1]]"
[[1 0 1]
[1 0 1]
[1 0 1]
[1 0 1]]
y = x + vv # Add x and vv elementwise
print(y)
[[ 2 2 4]
[ 5 5 7]
[ 8 8 10]
[11 11 13]]
Numpy broadcasting allows us to perform this computation without actually creating multiple copies of v. Consider this version, using broadcasting:
# We will add the vector v to each row of the matrix x,
# storing the result in the matrix y
x = np.array([[1,2,3], [4,5,6], [7,8,9], [10, 11, 12]])
v = np.array([1, 0, 1])
y = x + v # Add v to each row of x using broadcasting
print(y)
[[ 2 2 4]
[ 5 5 7]
[ 8 8 10]
[11 11 13]]
The line y = x + v works even though x has shape (4, 3) and v has shape (3,) due to broadcasting; this line works as if v actually had shape (4, 3), where each row was a copy of v, and the sum was performed elementwise.
Broadcasting two arrays together follows these rules:
- If the arrays do not have the same rank, prepend the shape of the lower rank array with 1s until both shapes have the same length.
- The two arrays are said to be compatible in a dimension if they have the same size in the dimension, or if one of the arrays has size 1 in that dimension.
- The arrays can be broadcast together if they are compatible in all dimensions.
- After broadcasting, each array behaves as if it had shape equal to the elementwise maximum of shapes of the two input arrays.
- In any dimension where one array had size 1 and the other array had size greater than 1, the first array behaves as if it were copied along that dimension
If this explanation does not make sense, try reading the explanation from the documentation.
Functions that support broadcasting are known as universal functions. You can find the list of all universal functions in the documentation.
Here are some applications of broadcasting:
# Compute outer product of vectors
v = np.array([1,2,3]) # v has shape (3,)
w = np.array([4,5]) # w has shape (2,)
# To compute an outer product, we first reshape v to be a column
# vector of shape (3, 1); we can then broadcast it against w to yield
# an output of shape (3, 2), which is the outer product of v and w:
print(np.reshape(v, (3, 1)) * w)
[[ 4 5]
[ 8 10]
[12 15]]
# Add a vector to each row of a matrix
x = np.array([[1,2,3], [4,5,6]])
# x has shape (2, 3) and v has shape (3,) so they broadcast to (2, 3),
# giving the following matrix:
print(x + v)
[[2 4 6]
[5 7 9]]
# Add a vector to each column of a matrix
# x has shape (2, 3) and w has shape (2,).
# If we transpose x then it has shape (3, 2) and can be broadcast
# against w to yield a result of shape (3, 2); transposing this result
# yields the final result of shape (2, 3) which is the matrix x with
# the vector w added to each column. Gives the following matrix:
print((x.T + w).T)
[[ 5 6 7]
[ 9 10 11]]
# Another solution is to reshape w to be a row vector of shape (2, 1);
# we can then broadcast it directly against x to produce the same
# output.
print(x + np.reshape(w, (2, 1)))
[[ 5 6 7]
[ 9 10 11]]
# Multiply a matrix by a constant:
# x has shape (2, 3). Numpy treats scalars as arrays of shape ();
# these can be broadcast together to shape (2, 3), producing the
# following array:
print(x * 2)
[[ 2 4 6]
[ 8 10 12]]
Broadcasting typically makes your code more concise and faster, so you should strive to use it where possible.
This brief overview has touched on many of the important things that you need to know about numpy, but is far from complete. Check out the numpy reference to find out much more about numpy.
Scipy
To be continued...
Matplotlib
Matplotlib is a plotting library. In this section give a brief introduction to the matplotlib.pyplot module, which provides a plotting system similar to that of MATLAB.
import matplotlib.pyplot as plt
By running this special iPython command, we will be displaying plots inline:
%matplotlib inline
Plotting
The most important function in matplotlib is plot, which allows you to plot 2D data. Here is a simple example:
# Compute the x and y coordinates for points on a sine curve
x = np.arange(0, 3 * np.pi, 0.1)
y = np.sin(x)
# Plot the points using matplotlib
plt.plot(x, y)
[<matplotlib.lines.Line2D at 0x1142b94d0>]
With just a little bit of extra work we can easily plot multiple lines at once, and add a title, legend, and axis labels:
y_sin = np.sin(x)
y_cos = np.cos(x)
# Plot the points using matplotlib
plt.plot(x, y_sin)
plt.plot(x, y_cos)
plt.xlabel('x axis label')
plt.ylabel('y axis label')
plt.title('Sine and Cosine')
plt.legend(['Sine', 'Cosine'])
<matplotlib.legend.Legend at 0x114390a50>
Subplots
You can plot different things in the same figure using the subplot function. Here is an example:
# Compute the x and y coordinates for points on sine and cosine curves
x = np.arange(0, 3 * np.pi, 0.1)
y_sin = np.sin(x)
y_cos = np.cos(x)
# Set up a subplot grid that has height 2 and width 1,
# and set the first such subplot as active.
plt.subplot(2, 1, 1)
# Make the first plot
plt.plot(x, y_sin)
plt.title('Sine')
# Set the second subplot as active, and make the second plot.
plt.subplot(2, 1, 2)
plt.plot(x, y_cos)
plt.title('Cosine')
# Show the figure.
plt.show()
You can read much more about the subplot function in the documentation.
Holoviews
To be continued...
Performance
Class Matrix
import random
class Matrix(list):
@classmethod
def zeros(cls, shape):
n_rows, n_cols = shape
return cls([[0] * n_cols for i in range(n_rows)])
@classmethod
def random(cls, shape):
M, (n_rows, n_cols) = cls(), shape
for i in range(n_rows):
M.append([random.randint(-255, 255)
for j in range(n_cols)])
return M
def transpose(self):
n_rows, n_cols = self.shape
return self.__class__(zip(*self))
@property
def shape(self):
return ((0, 0) if not self else
(len(self), len(self[0])))
def matrix_product(X, Y):
"""Computes the matrix product of X and Y.
>>> X = Matrix([[1], [2], [3]])
>>> Y = Matrix([[4, 5, 6]])
>>> matrix_product(X, Y)
[[4, 5, 6], [8, 10, 12], [12, 15, 18]]
>>> matrix_product(Y, X)
[[32]]
"""
n_xrows, n_xcols = X.shape
n_yrows, n_ycols = Y.shape
# верим, что с размерностями всё хорошо
Z = Matrix.zeros((n_xrows, n_ycols))
for i in range(n_xrows):
for j in range(n_xcols):
for k in range(n_ycols):
Z[i][k] += X[i][j] * Y[j][k]
return Z
%doctest_mode
Exception reporting mode: Plain
Doctest mode is: ON
>>> X = Matrix([[1], [2], [3]])
>>> Y = Matrix([[4, 5, 6]])
>>> matrix_product(X, Y)
[[4, 5, 6], [8, 10, 12], [12, 15, 18]]
>>> matrix_product(Y, X)
[[32]]
[[32]]
%doctest_mode
Exception reporting mode: Context
Doctest mode is: OFF
Runtime measurement
Everything seems to work, but how fast? Use the magic timeit command to check.
%%timeit shape = 64, 64; X = Matrix.random(shape); Y = Matrix.random(shape)
matrix_product(X, Y)
86.6 ms ± 1.52 ms per loop (mean ± std. dev. of 7 runs, 10 loops each)
Total: Multiplying two 64x64 matrices takes near 0.1 seconds. Y U SO SLOW?
We define an auxiliary function bench, which generates random matrices of the specified size, and then n_iter times multiplies them in a loop.
def bench(shape=(64, 64), n_iter=16):
X = Matrix.random(shape)
Y = Matrix.random(shape)
for iter in range(n_iter):
matrix_product(X, Y)
Let's try to look at it more closely with the help of the line_profiler module.
#!pip install line_profiler
%load_ext line_profiler
%lprun -f matrix_product bench()
Note that the operation list .__ getitem__ is not free. Swap the for loops so that the code does less index lookups.
def matrix_product(X, Y):
n_xrows, n_xcols = X.shape
n_yrows, n_ycols = Y.shape
Z = Matrix.zeros((n_xrows, n_ycols))
for i in range(n_xrows):
Xi = X[i]
for k in range(n_ycols):
acc = 0
for j in range(n_xcols):
acc += Xi[j] * Y[j][k]
Z[i][k] = acc
return Z
%lprun -f matrix_product bench()
2 seconds faster, but still too slow:> 30% of the time goes exclusively to iteration! Fix it.
def matrix_product(X, Y):
n_xrows, n_xcols = X.shape
n_yrows, n_ycols = Y.shape
Z = Matrix.zeros((n_xrows, n_ycols))
for i in range(n_xrows):
Xi, Zi = X[i], Z[i]
for k in range(n_ycols):
Zi[k] = sum(Xi[j] * Y[j][k] for j in range(n_xcols))
return Z
%lprun -f matrix_product bench()
The matrix_product functions are pretty prettier. But, it seems, this is not the limit. Let’s try again to remove unnecessary index calls from the innermost cycle.
def matrix_product(X, Y):
n_xrows, n_xcols = X.shape
n_yrows, n_ycols = Y.shape
Z = Matrix.zeros((n_xrows, n_ycols))
Yt = Y.transpose() # <--
for i, (Xi, Zi) in enumerate(zip(X, Z)):
for k, Ytk in enumerate(Yt):
Zi[k] = sum(Xi[j] * Ytk[j] for j in range(n_xcols))
return Z
Numba
Numba does not work with inline lists. Rewrite the matrix_product function using ndarray.
import numba
import numpy as np
@numba.jit
def jit_matrix_product(X, Y):
n_xrows, n_xcols = X.shape
n_yrows, n_ycols = Y.shape
Z = np.zeros((n_xrows, n_ycols), dtype=X.dtype)
for i in range(n_xrows):
for k in range(n_ycols):
for j in range(n_xcols):
Z[i, k] += X[i, j] * Y[j, k]
return Z
Let's see what happened.
shape = 64, 64
X = np.random.randint(-255, 255, shape)
Y = np.random.randint(-255, 255, shape)
%timeit -n100 jit_matrix_product(X, Y)
The slowest run took 21.46 times longer than the fastest. This could mean that an intermediate result is being cached.
495 µs ± 900 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)
Cython
%load_ext cython
%%capture
%%cython -a
import random
class Matrix(list):
@classmethod
def zeros(cls, shape):
n_rows, n_cols = shape
return cls([[0] * n_cols for i in range(n_rows)])
@classmethod
def random(cls, shape):
M, (n_rows, n_cols) = cls(), shape
for i in range(n_rows):
M.append([random.randint(-255, 255)
for j in range(n_cols)])
return M
def transpose(self):
n_rows, n_cols = self.shape
return self.__class__(zip(*self))
@property
def shape(self):
return ((0, 0) if not self else
(int(len(self)), int(len(self[0]))))
def cy_matrix_product(X, Y):
n_xrows, n_xcols = X.shape
n_yrows, n_ycols = Y.shape
Z = Matrix.zeros((n_xrows, n_ycols))
Yt = Y.transpose()
for i, Xi in enumerate(X):
for k, Ytk in enumerate(Yt):
Z[i][k] = sum(Xi[j] * Ytk[j] for j in range(n_xcols))
return Z
X = Matrix.random(shape)
Y = Matrix.random(shape)
%timeit -n100 cy_matrix_product(X, Y)
21.4 ms ± 1.36 ms per loop (mean ± std. dev. of 7 runs, 100 loops each)
The problem is that Cython cannot efficiently optimize work with lists that can contain elements of various types, so we rewrite matrix_product using ndarray.
X = np.random.randint(-255, 255, size=shape)
Y = np.random.randint(-255, 255, size=shape)
%%capture
%%cython -a
import numpy as np
def cy_matrix_product(X, Y):
n_xrows, n_xcols = X.shape
n_yrows, n_ycols = Y.shape
Z = np.zeros((n_xrows, n_ycols), dtype=X.dtype)
for i in range(n_xrows):
for k in range(n_ycols):
for j in range(n_xcols):
Z[i, k] += X[i, j] * Y[j, k]
return Z
%timeit -n100 cy_matrix_product(X, Y)
176 ms ± 4.65 ms per loop (mean ± std. dev. of 7 runs, 100 loops each)
How so! It just got worse, with most of the code still using Python calls. Let's get rid of them by annotating the code with types.
%%capture
%%cython -a
import numpy as np
cimport numpy as np
def cy_matrix_product(np.ndarray X, np.ndarray Y):
cdef int n_xrows = X.shape[0]
cdef int n_xcols = X.shape[1]
cdef int n_yrows = Y.shape[0]
cdef int n_ycols = Y.shape[1]
cdef np.ndarray Z
Z = np.zeros((n_xrows, n_ycols), dtype=X.dtype)
for i in range(n_xrows):
for k in range(n_ycols):
for j in range(n_xcols):
Z[i, k] += X[i, j] * Y[j, k]
return Z
%timeit -n100 cy_matrix_product(X, Y)
173 ms ± 4 ms per loop (mean ± std. dev. of 7 runs, 100 loops each)
Unfortunately, typical annotations did not change the run time, because the body of the nested Cython itself could not optimize. Fatality-time: indicate the type of elements in ndarray.
%%capture
%%cython -a
import numpy as np
cimport numpy as np
def cy_matrix_product(np.ndarray[np.int64_t, ndim=2] X,
np.ndarray[np.int64_t, ndim=2] Y):
cdef int n_xrows = X.shape[0]
cdef int n_xcols = X.shape[1]
cdef int n_yrows = Y.shape[0]
cdef int n_ycols = Y.shape[1]
cdef np.ndarray[np.int64_t, ndim=2] Z = \
np.zeros((n_xrows, n_ycols), dtype=np.int64)
for i in range(n_xrows):
for k in range(n_ycols):
for j in range(n_xcols):
Z[i, k] += X[i, j] * Y[j, k]
return Z
%timeit -n100 cy_matrix_product(X, Y)
541 µs ± 5.14 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)
Let's try to go further and disable checks for going beyond the boundaries of the array and overflow of integer types.
%%capture
%%cython -a
import numpy as np
cimport cython
cimport numpy as np
@cython.boundscheck(False)
@cython.overflowcheck(False)
def cy_matrix_product(np.ndarray[np.int64_t, ndim=2] X,
np.ndarray[np.int64_t, ndim=2] Y):
cdef int n_xrows = X.shape[0]
cdef int n_xcols = X.shape[1]
cdef int n_yrows = Y.shape[0]
cdef int n_ycols = Y.shape[1]
cdef np.ndarray[np.int64_t, ndim=2] Z = \
np.zeros((n_xrows, n_ycols), dtype=np.int64)
for i in range(n_xrows):
for k in range(n_ycols):
for j in range(n_xcols):
Z[i, k] += X[i, j] * Y[j, k]
return Z
%timeit -n100 cy_matrix_product(X, Y)
226 µs ± 2.84 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)
Numpy
import numpy as np
X = np.random.randint(-255, 255, shape)
Y = np.random.randint(-255, 255, shape)
%timeit -n100 X.dot(Y)
151 µs ± 4.01 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)
%timeit -n100 X*Y
6.02 µs ± 1.54 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)
Profit.
Multithreading and GIL
|| minimum
Process
- Process - running program.
- Each process has a state isolated from other processes:
-
- virtual address space,
-
- pointer to executable instruction,
-
- call stack,
-
- system resources, such as open file descriptors.
- Processes are convenient for simultaneously performing multiple tasks.
- Alternative way: delegate each task to a thread.
Thread
- A thread is similar to a process in that its execution occurs independently of other threads (and processes).
- Unlike a process, a thread executes within a process and shares the address space and system resources with it.
- Threads are convenient for simultaneously performing several tasks that require access to a shared state.
- The joint execution of several processes and threads is controlled by the operating system, sequentially allowing each process or thread to use some processor cycles.
threading module
- A thread in Python is a system thread, that is, it is not the interpreter that controls its execution, but the operating system.
- You can create a thread using the
Threadclass from the module of the standardthreadinglibrary.
import time
from threading import Thread
def countdown(n):
for i in range(n):
print(n - i - 1, "left")
time.sleep(1)
t = Thread(target=countdown, args=(3,))
t.start()
2 left
An alternative way to create a stream is inheritance:
class CountdownThread(Thread):
def __init__(self, n):
super().__init__()
self.n = n
def run(self): # start method.
for i in range(self.n):
print(self.n - i - 1, "left")
time.sleep(1)
t = CountdownThread(3)
t.start()
2 left
The disadvantage of this approach is that it limits the reuse of code: the functionality of the CountdownThread class can be used only in a separate thread.
- When creating a stream, you can specify a name. By default it is 'Thread-N':
Thread().name
'Thread-6'
Thread(name="NumberCruncher").name
'NumberCruncher'
- Each active thread has an id - a non-negative number unique to all active threads.
t = Thread()
t.start()
t.ident
123145519448064
- The
joinmethod allows you to wait until the stream finishes. -
- The execution of the calling thread will pause until thread t ends.
-
- Repeated calls to the
joinmethod have no effect.
- Repeated calls to the
t = Thread(target=time.sleep, args=(5, ))
t.start()
t.join() # locks for 5 seconds
t.join() # performed instantly
1 left
1 left
0 left
0 left
- You can check if the thread is running using the
is_alivemethod:
t = Thread(target=time.sleep, args=(5, ))
t.start()
t.is_alive() # False after 5 seconds
True
-
A daemon is a thread created with the
daemon=Trueargument: -
The difference between a daemon thread and a regular thread is that daemon threads are automatically destroyed when exiting the interpreter.
t = Thread(target=time.sleep, args=(5,), daemon=True)
t.start()
t.daemon
True
- In Python, there is no built-in mechanism for terminating threads - this is not an accident, but an informed decision of the language developers.
- Correct termination of the flow is often associated with the release of resources, for example:
-
- a stream can work with a file whose descriptor needs to be closed,
-
- or capture a synchronization primitive.
- To end a stream, a flag is usually used:
class Task:
def __init__(self):
self._running = True
def terminate(self):
self._running = False
def run(self, n):
while self._running:
...
The set of synchronization primitives in the threading module is standard:
Lock- a regular mutex, used to provide exclusive access to a shared state.RLock- a recursive mutex that allows a thread that owns a mutex to capture the mutex more than once.Semaphore- a variation of the mutex that allows you to capture yourself no more than a fixed number of times.BoundedSemaphore- a semaphore that makes sure that it is captured and released the same number of times.
All synchronization primitives implement a single interface:
- the acquire method captures the synchronization primitive,
- and the release method releases it.
class SharedCounter:
def __init__(self, value):
self._value = value
self._lock = Lock()
def increment(self, delta=1):
self._lock.acquire()
self._value += delta
self._lock.release()
def get(self):
return self._value
queue module
The queue module implements several thread-safe queues:
Queue- FIFO queue,LifoQueue— LIFO queue of stacks,PriorityQueue— a queue of elements — a parse (priority, item).- There are no special frills in the implementation of queues: all state-changing methods work “inside” the mutex.
- The
Queueclass usesdequeas the container, and theLifoQueueandPriorityQueueclasses use the list.
def worker(q):
while True:
item = q.get() # blocking expects next
do_something(item) # element
q.task_done() # notifies the execution queue
def master(q):
for item in source():
q.put(item)
# blocking waits until all elements of the queue
# will not be processed
q.join()
futures module
- The
concurrent.futuresmodule contains the abstract classExecutorand its implementation as a thread pool -ThreadPoolExecutor. - The executor’s interface consists of only three methods:
from concurrent.futures import *
executor = ThreadPoolExecutor(max_workers=4)
executor.submit(print, "Hello, world!")
Hello, world!
<Future at 0x1043b1d90 state=running>
list(executor.map(print, ["Knock?", "Knock!"]))
Knock?
Knock!
[None, None]
executor.shutdown()
- Contractors support the context manager protocol:
with ThreadPoolExecutor(max_workers=4) as executor:
...
- The
Executor.submitmethod returns an instance of theFutureclass that encapsulates asynchronous calculations.
What can be done with Future?
with ThreadPoolExecutor(max_workers=4) as executor:
f = executor.submit(sorted, [4, 3, 1, 2])
- Ask about the calculation status:
f.running(), f.done(), f.cancelled()
(False, True, False)
- Wait for the blocking result of the calculation:
print(f.result())
[1, 2, 3, 4]
print(f.exception())
None
- Add a function that will be called after the calculation is completed:
f.add_done_callback(print)
<Future at 0x1043b7f10 state=finished returned list>
futures module example: integrate
import math
def integrate(f, a, b, *, n_iter=1000):
acc = 0
step = (b - a) / n_iter
for i in range(n_iter):
acc += f(a + i * step) * step
return acc
integrate(math.cos, 0, math.pi / 2)
1.0007851925466296
from functools import partial
def integrate_async(f, a, b, *, n_jobs, n_iter=1000):
executor = ThreadPoolExecutor(max_workers=n_jobs)
spawn = partial(executor.submit, integrate, f,
n_iter=n_iter // n_jobs)
step = (b-a)/n_jobs
fs=[spawn(a+i*step,a+(i+1)*step)
for i in range(n_jobs)]
return sum(f.result() for f in as_completed(fs))
integrate_async(math.cos, 0, math.pi / 2, n_jobs=2)
1.0007851925466305
Concurrency and Competition
Compare the performance of the serial and parallel versions of the integrate function using the “magic” timeit command:
%%timeit -n100
integrate(math.cos, 0, math.pi / 2, n_iter=10**6)
154 ms ± 2.28 ms per loop (mean ± std. dev. of 7 runs, 100 loops each)
%%timeit -n100
integrate_async(math.cos, 0, math.pi / 2, n_iter=10**6, n_jobs=2)
142 ms ± 2.11 ms per loop (mean ± std. dev. of 7 runs, 100 loops each)
GIL
- GIL (global interpreter lock) is a mutex that ensures that only one thread at a time has access to the internal state of the interpreter.
- The Python C API allows you to release the GIL, but it is only safe when working with objects that are not dependent on the Python interpreter.
Is GIL Bad?
- The answer depends on the task.
- The presence of GIL makes it impossible to use threads in Python for parallelism: several threads do not speed up, and sometimes even slow down the program.
- GIL does not interfere with the use of threads for competition when working with I/O.
C and Cython - GIL Remedy
%load_ext Cython
%%cython
from libc.math cimport cos
def integrate(f, double a, double b, long n_iter):
cdef double acc = 0
cdef double step=(b-a)/n_iter
cdef long i
with nogil:
for i in range(n_iter):
acc += cos(a + i * step) * step
return acc
%%timeit -n100
integrate_async(math.cos, 0, math.pi / 2, n_iter=10**6, n_jobs=2)
5.88 ms ± 126 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)
multiprocessing module
Processes Another GIL Remedy
- You can use processes instead of threads.
- Each process will have its own GIL, but it will not prevent them from working in parallel.
- The
multiprocessingmodule is responsible for working with processes in Python:
import multiprocessing as mp
p = mp.Process(target=countdown, args=(5, ))
p.start()
4 left
3 left
2 left
1 left
0 left
- The module implements basic synchronization primitives: mutexes, semaphores, conditional variables.
- To organize the interaction between processes, you can use
Pipe- a socket-based connection between two processes:
def ponger(conn):
conn.send("pong")
parent_conn, child_conn = mp.Pipe()
p = mp.Process(target=ponger, args=(child_conn, ))
p.start()
parent_conn.recv()
'pong'
p.join()
Process and performance
The implementation of the integrate_async function based on the thread pool worked for a long time, let's try to use the process pool:
from concurrent.futures import ProcessPoolExecutor
def integrate_async(f, a, b, *, n_jobs, n_iter=1000):
executor = ProcessPoolExecutor(max_workers=n_jobs)
spawn = partial(executor.submit, integrate, f,
n_iter=n_iter // n_jobs)
step = (b - a) / n_jobs
fs=[spawn(a + i * step, a + (i + 1) * step)
for i in range(n_jobs)]
return sum(f.result() for f in as_completed(fs))
%%timeit -n100
integrate_async(math.cos, 0, math.pi / 2, n_iter=10**6, n_jobs=2)
16.6 ms ± 144 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)
joblib package
The joblib package implements a parallel analogue of the for loop, which is convenient for parallel execution of independent tasks.
from joblib import Parallel, delayed
def integrate_async(f, a, b, *, n_jobs, n_iter=1000, backend=None):
step = (b - a) / n_jobs
with Parallel(n_jobs=n_jobs, backend=backend) as parallel:
fs = (delayed(integrate)(f, a + i * step,
a + (i + 1) * step,
n_iter=n_iter // n_jobs)
for i in range(n_jobs))
return sum(parallel(fs))
%%timeit -n100
integrate_async(math.cos, 0, math.pi / 2, n_iter=10**6, n_jobs=2, backend="threading")
104 ms ± 280 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)
%%timeit -n100
integrate_async(math.cos, 0, math.pi / 2, n_iter=10**6, n_jobs=2, backend="multiprocessing")
290 ms ± 1.13 ms per loop (mean ± std. dev. of 7 runs, 100 loops each)
Summary
- GIL is a global mutex that limits the use of threads for parallelism in programs in Python.
- For programs that use mainly I / O, GIL is not scary: in CPython, these operations release the GIL.
- For programs that need parallelism, there are options for increasing productivity:
-
- write critical functionality in C or Cython;
-
- or use the multiprocessing module.
numba JIT compiler
import math
from numba import jit, prange
@jit(nopython=True, parallel=True, fastmath=True, cache=True)
def integrate(a, b, *, n_iter=1000):
acc = 0
step = (b - a) / n_iter
for i in prange(n_iter):
acc += math.cos(a + i * step) * step
return acc
%%timeit -n100
integrate(0, math.pi / 2, n_iter=10**6)
5.11 ms ± 983 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)
Profit.
Async python
Нам предстоит погрузиться в мир асинхронного программирования. Сейчас уже сложно представить Python без асинхронного подхода — он только набирает популярность среди веб-разработчиков.
Итераторы
Разработчики используют итераторы в коде настолько часто, что даже не задумываются, в чём они помогают. Итераторы в Python — это списки, словари, множества, строки, файлы и другие коллекции. Везде, где вы пишете цикл for, используется итератор. Итераторы помогают перемещаться по объектам любого контейнера в коде. При этом вам не нужно задумываться о том, как хранятся и обрабатываются эти элементы: итератор инкапсулирует их. Проще говоря, это способ вычитывать элементы из объекта по одному.
Перейдём сразу к практике. Представим, что на собеседовании вас попросили реализовать аналог функции range.
class Range:
def __init__(self, stop_value: int):
self.current = -1
self.stop_value = stop_value - 1
def __iter__(self):
return RangeIterator(self)
class RangeIterator:
def __init__(self, container):
self.container = container
def __next__(self):
if self.container.current < self.container.stop_value:
self.container.current += 1
return self.container.current
raise StopIteration
Получили первую версию работающего кода. Запустим код и убедимся в этом.
_range = Range(5)
for i in _range:
print(i)
0
1
2
3
4
«А как это работает? Расскажите подробнее»
Начнём с класса Range. У него внутри реализован магический метод __iter__. Он обозначает, что объект этого класса итерабельный, то есть с ним можно работать в цикле for. Ещё говорят, что __iter__ отдаёт итерируемый объект.
Ограничимся понятиями итератора и итерабельного объекта. Чтобы код действительно отдавал новые данные из range, нужно реализовать соответствующую функцию. Она как раз и называется итератор. RangeIterator — итератор для класса range. Любой итератор должен реализовывать магическую функцию __next__, в которой он должен отдавать новые значения для объектов класса Range. Если вы дошли до конца множества значений, то появляется исключение StopIteration.
Для тех, кто привык читать первоисточники, существует PEP-234 (на английском). Там подробно изложена работа итераторов и итерабельных объектов.
Но можно ли как-то упростить написанный выше код? Да, можно.
class Range2:
def __init__(self, stop_value: int):
self.current = -1
self.stop_value = stop_value - 1
def __iter__(self):
return self
def __next__(self):
if self.current < self.stop_value:
self.current += 1
return self.current
raise StopIteration
В Python есть возможность объявить объекты класса и итерабельными, и итераторами. Это удобно, но с точки зрения принципов проектирования приложения, у такого объекта есть две ответственности: он является итератором и при этом выполняет какую-то свою логику. В мире Python это допустимо, но в некоторых других языках вас могут понять неправильно. Будьте бдительны!
Ещё стоит рассмотреть, как работает цикл for под капотом.
iterable = Range2(5)
iterator = iter(iterable)
while True:
try:
value = next(iterator)
print(value)
except StopIteration:
break
0
1
2
3
4
Генераторы
Работа генераторов построена на принципе запоминания контекста выполнения функции. Если не вдаваться в подробности работы Python-интерпретатора, то функция-генератор «запоминает», на каком месте она остановилась, и может продолжить своё выполнение после ключевого слова yield.
Рассмотрим простой пример.
def simple_generator():
yield 1
yield 2
return 3
Посмотрим, что будет, если вызвать такой код:
gen = simple_generator()
print(next(gen))
print(next(gen))
print(next(gen))
1
2
---------------------------------------------------------------------------
StopIteration Traceback (most recent call last)
Cell In[7], line 4
2 print(next(gen))
3 print(next(gen))
----> 4 print(next(gen))
StopIteration: 3
То есть функция действительно запоминает, где она остановилась после каждого вызова функции next.
Генераторы удобны и для создания генераторных выражений — generator expressions. Особенно это полезно, если нужно сгенерировать много объектов, а память расходовать жалко. Код выглядит так:
gen_exp = (x for x in range(100000))
print(gen_exp)
<generator object <genexpr> at 0x7dbe33f1dfc0>
Есть ещё небольшой синтаксический сахар, связанный с генераторами. Представим функцию, внутри которой есть цикл по элементам списка, и они выводятся один за другим.
numbers = [1, 2, 3]
def func():
for item in numbers:
yield item
for item in func():
print(item)
1
2
3
За счёт генератора конструкция сокращается до такой:
def func():
yield from numbers
Бывает очень полезно, но на практике используется довольно редко.
Корутины
Затронем тему корутин — основных строительных блоков асинхронного программирования на Python. Они появились в ответ на невозможность использования полноценного распараллеливания программы с помощью тредов (потоков) из-за работы GIL. Для тех, кому интересно узнать подробнее про Global Interpreter Lock, есть хорошая обзорная статья.
Корутина — это генератор. Однако в PEP-342 предложили расширить возможности генераторов, добавив туда несколько конструкций, о которых сейчас пойдёт речь.
Представьте себе метод, который на вход получает какое-то значение, как-то его обрабатывает и отдаёт результат. Пусть это будет функция, рассчитывающая количество денег на вашем счете через $N$ лет при определённом проценте. На вход функция принимает процент по депозиту в годовых и сумму на счёте.
import math
def cash_return(deposit: int, percent: float, years: int) -> float:
value = math.pow(1 + percent / 100, years)
return round(deposit * value, 2)
Теперь узнаем, сколько вы получите денег через $5$ лет, если сумма на депозите — $1 000 000$ рублей, а ставка по депозиту — $5%%$ годовых.
cash_return(1_000_000, 5, 5)
1276281.56
Теперь вы хотите посмотреть на то, как будет меняться итоговая сумма в зависимости от депозита. Тут приходит на помощь корутина.
import math
def cash_return_coro(percent: float, years: int) -> float:
value = math.pow(1 + percent / 100, years)
while True:
try:
deposit = (yield)
yield round(deposit * value, 2)
except GeneratorExit:
print('Выход из корутины')
raise
Запустим корутину с теми же условиями — $5$ лет и $5%%$ годовых.
coro = cash_return_coro(5, 5)
next(coro)
values = [1000, 2000, 5000, 10000, 100000]
for item in values:
print(coro.send(item))
next(coro)
coro.close()
1276.28
2552.56
6381.41
12762.82
127628.16
Выход из корутины
Разберёмся, что произошло. В коде видно четыре новых конструкции: (yield), send(...), close() и GeneratorExit. Корутины могут не только отдавать значения и запоминать место, где остановился код, но и ждать новых значений. Для этого ввели конструкцию (yield), которая позволяет принимать набор параметров. Так как приём параметров в корутине происходит необычным способом, то и отправка параметров сделана с помощью специальной функции send(...), через которую можно передать в функцию необходимые параметры. В конце ещё можно вызвать метод close(), который прекратит выполнение корутины. Когда вы вызываете метод close(), выбрасывается исключение GeneratorExit, которое можно перехватить и грамотно обработать.
Ещё одно преимущество — возможность запомнить контекст выполнения. В функции cash_return_coro нет необходимости вычислять переменную value каждый раз, когда вы хотите посчитать сумму. Недостатком такого подхода можно назвать большее количество кода, который надо написать, чтобы всё могло грамотно работать.
Асинхронное программирование
Асинхронное программирование в мире Python-разработки на пике популярности. Про него пишут статьи и делают доклады на конференциях. Концепция уже прижилась и во многих других популярных языках. Давайте восполним пробелы и погрузимся в работу с асинхронным кодом на Python.
Работа с разными типами задач
Раньше разработчики не сильно заостряли своё внимание на типе выполняемых задач внутри приложения — это было не нужно для индустрии в целом. Все писали достаточно большие монолитные приложения, а проблемы с производительностью обычно решались на уровне горизонтального масштабирования: через потоки, процессы или даже через несколько приложений на разных виртуальных машинах.
Сейчас использование только процессов и потоков не даёт нужной производительности. Рассмотрим три основных типа задач, с которыми сталкивается большинство разработчиков:
-
CPU bound-задачи. Задачи, для которых необходимо интенсивное использование процессора. К ним относят использование сложных математических моделей, обучение нейронных сетей, рендеринг графики и вычисление хэшей.
-
I/O bound-задачи (non-RAM I/O bound). Задачи, в которых основная часть работы приходится на ввод/вывод информации I/O или input/output. В основном такие задачи относятся к работе с файловой системой и с сетью.
-
Memory bound-задачи (RAM I/O bound). Задачи, в которых происходит интенсивная работа с оперативной памятью. Как правило, такие задачи появляются в сложных математических моделях. Из-за медленной работы с оперативной памятью всё больше моделей обрабатывают с помощью видеокарт, в которых работа с памятью устроена по-другому. Другой пример — обработка огромного объёма данных в Map-Reduce-системах, например, таких как Spark. Обработка будет идти быстрее, если оперативной памяти будет больше.
Подробнее об этом можно прочитать в англоязычных статьях: - о значении терминов CPU bound и I/O bound, - о производительности.
Из-за массового перехода на микросервисы количество сетевого взаимодействия между системами многократно возросло, как и нагрузка на базы данных. Проблемы работы с сетью или с доступом к БД относятся к I/O bound-задачам. То есть их основная работа — ожидание обработки запроса к внешней системе. Такой класс задач в монолитных системах решался пулом потоков — thread pool. Однако, его стало не хватать из-за достаточно интенсивной нагрузки на сеть между множеством сервисов.
Классический метод решения I/O bound задач — добавление ресурсов к существующим системам. Однако, многие компании не могут позволить себе «заливать всё железом» — докупать новые железные серверы, вместо оптимизации кода. Например, Instagram может себе такое позволить, поэтому они до сих пор используют Django даже с учётом всей нагрузки.
Перейдём к практике. Представьте приложение, которое ходит на некий сайт-агрегатор, достаёт данные по фильмам и сохраняет в БД. Код будет выглядеть так (ссылка на сайт выдуманная):
import requests
def do_some_logic(data):
pass
def save_to_database(data):
pass
data = requests.get('https://data.aggregator.com/films')
processed_data = do_some_logic(data)
save_to_database(data)
Этот код достаточно линейный. Если вместо загрузки фильмов в БД такой код будет выполнять отдачу данных о фильмах с этого же сайта, то при достаточной нагрузке приложение начнёт сильно проседать по скорости ответа клиентам. При этом бо́льшую часть времени код будет просто ждать запроса от клиента, делать запрос к сайту https://data.aggregator.com/films и отдавать данные. То есть в эти моменты интерпретатор не будет делать никаких полезных действий, а клиенты будут ждать.
Схематично изобразить выполнение программы можно вот так:
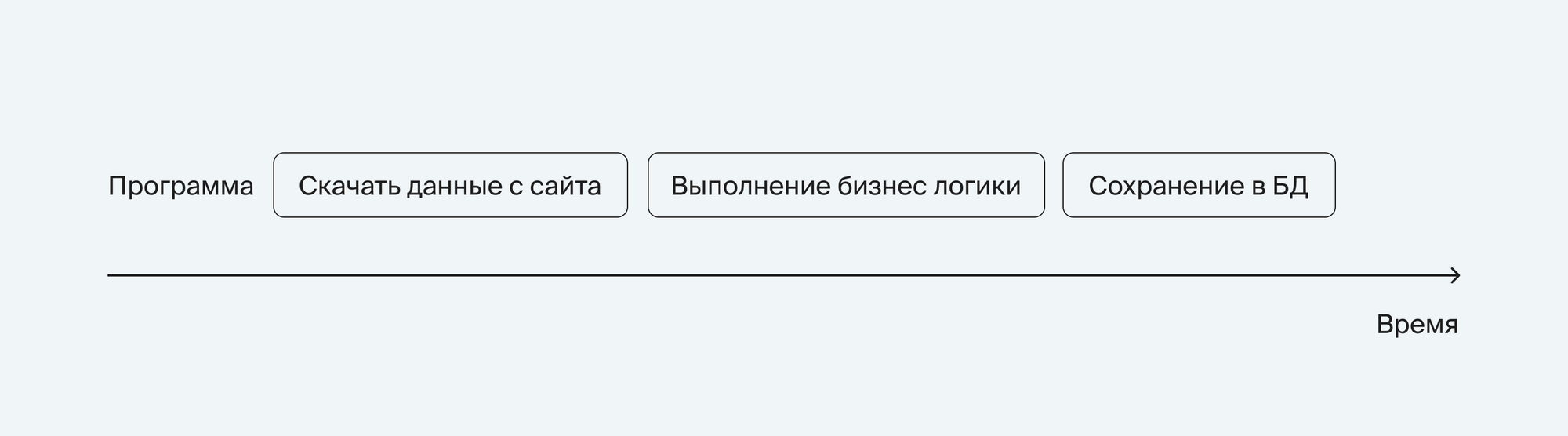
Теперь определим тип задачи в каждой ячейке:
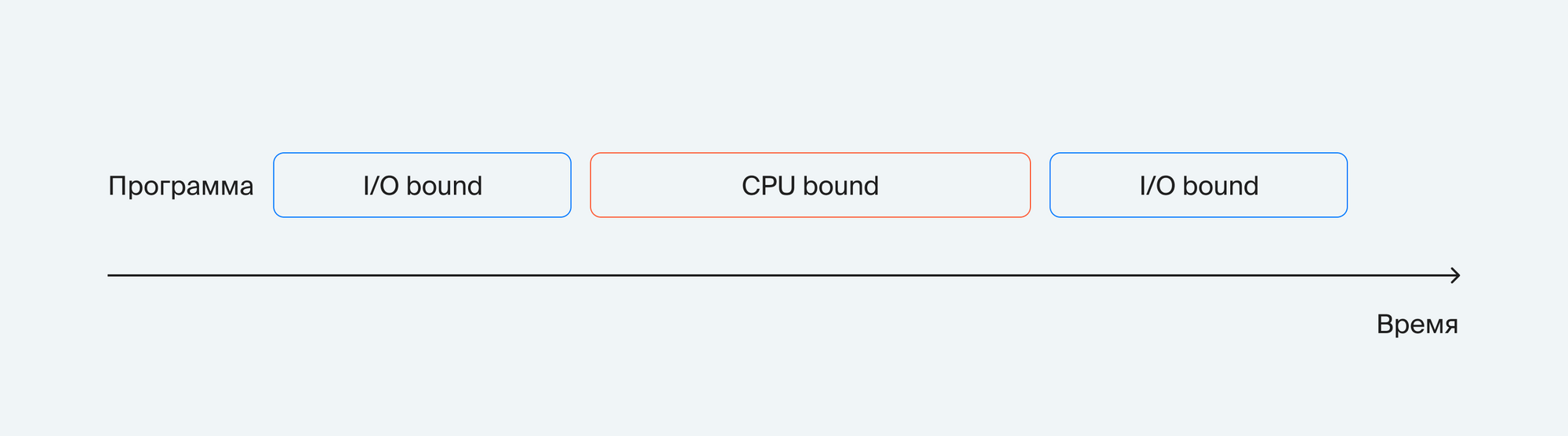
Интуитивно выполнение программы кажется примерно таким, как указано на картинке выше.

Однако, если привести картинку в соответствие с реальностью, получим следующий результат:
То есть бо́льшую часть времени программа ждёт ввода/вывода, а меньшая часть времени отводится на выполнение полезной работы.
Эту проблему можно решить, распараллелив код на процессы и потоки. Такой вариант поможет, но на короткое время — при таком подходе сильно увеличатся расходы ресурсов сервера. Плюс количество допустимых процессов и потоков ограничено. То есть либо закончится оперативная память под потоки, либо закончатся ядра под процессы. Вишенкой на торте становится GIL, который даёт работать только одному потоку в единицу времени. Это не позволяет эффективно использовать массовый параллелизм на потоках и добавляет свои накладные расходы, хоть и не очень заметные.
Посмотрим, как применение потоков сказывается на выполнении программы:
Действительно, два потока почти в два раза лучше отрабатывают I/O bound задачи. Но к сожалению, при таком подходе очень просто ошибиться и столкнуться с проблемой «состояния гонок». Можно попробовать вариант с корутинами, но его сложнее реализовать. И при таком способе не получится создать много потоков, так как они потребляют гораздо больше ОЗУ, чем корутины. Также написание многопоточного кода требует от разработчика большей внимательности, чем при написании линейного.
Стоит внимательнее присмотреться к проблеме. Всё ещё бо́льшую часть времени интерпретатор не совершает активных действий, а только ждёт ответа от ОС, завершилась ли та или иная операция ввода/вывода. В целом процессы и потоки не сильно помогут, ведь интерпретатор будет по-прежнему простаивать на каждом из них. При этом появится много накладных расходов на переключение контекста между процессами или на потребление оперативной памяти потоками, что может только ухудшить положение.
Все эти проблемы необходимо решать эффективно. С этим может помочь использование асинхронного кода.
Event-loop
Итак, вы добрались до сердца асинхронных программ в Python — цикла событий. Чтобы понять, как он работает, обратимся к простой реализации, которую предложил Девид Бизли (David Beazley) в 2009 году. Она хороша тем, что не содержит сложных конструкций, которыми сейчас обросли популярные реализации цикла событий на Python. Эта часть будет построена на разборе кода и практик, которые применяются для разработки цикла событий на основе кода Бизли, и как учитывать эти знания при разработке асинхронных приложений на Python. Код уже приведён к современной версии Python.
Начнём с архитектуры цикла событий.
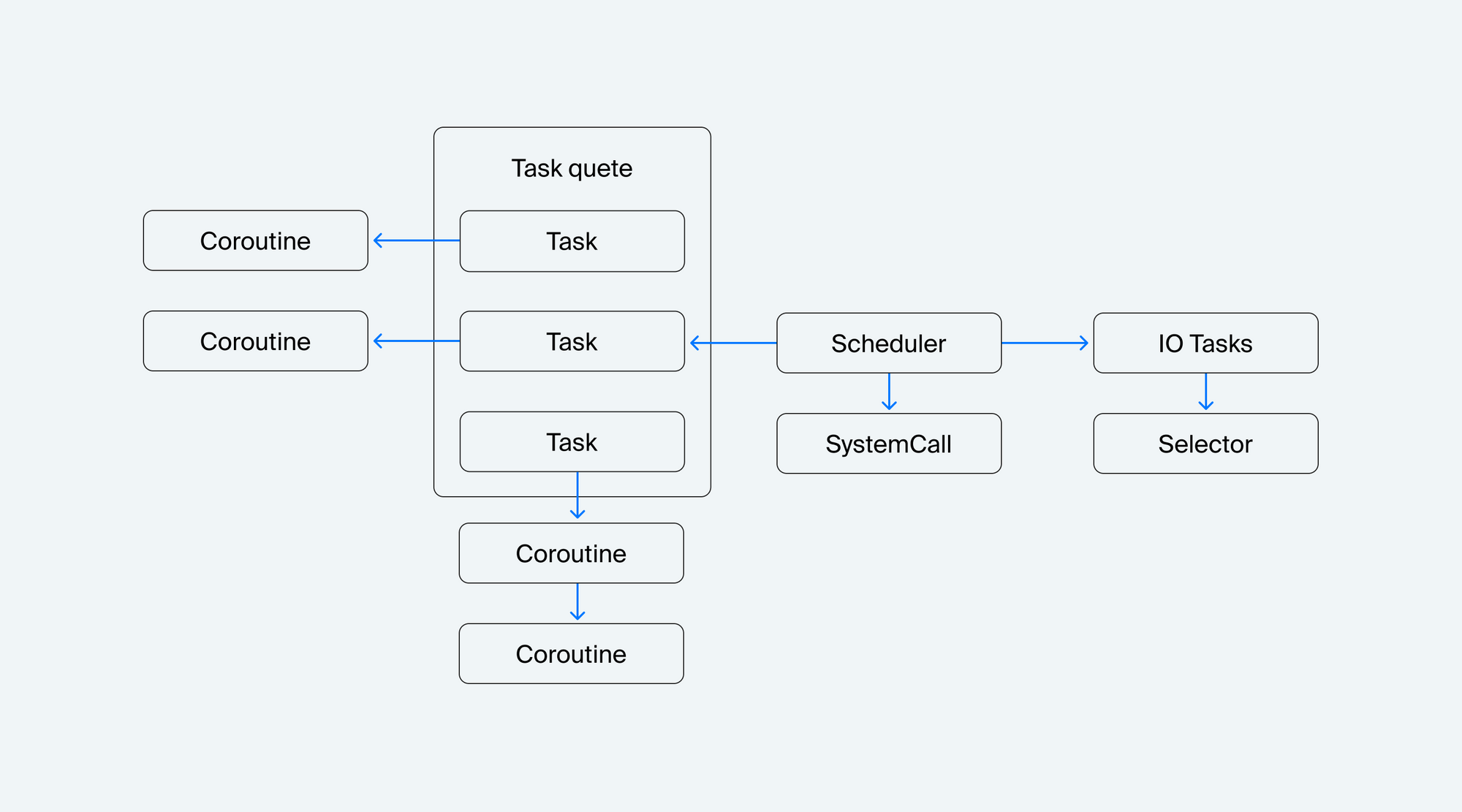
Расмотрим блоки:
- Планировщик (Scheduler). Корень всей программы. Обрабатывает задачи в очереди задач и следит за их правильным переключением между собой.
- Очередь задач (Task queue). Здесь собираются новые задачи на исполнение.
- Задача (Task). Основной блок работы цикла событий. В задачах хранится информация о выполняемой корутине. Умеет обрабатывать цепочку вложенных корутин.
- Корутина (Coroutine). Исполняемый код, которым оперирует планировщик задач.
- Системный вызов (SystemCall). Блоки кода, которые расширяют функциональность планировщика.
- Корутина для выполнения работы с I/O (I/O-tasks). В планировщик добавляется специальная задача (Task) для обработки I/O-событий от ОС.
- Селектор (Selector). Он слушает события от ОС и передаёт работу корутинам, которые ждут обработки I/O-сообщений.
Первым стоит рассмотреть работу планировщика. Его основные функции — приём и справедливая обработка списка задач.
import logging
from typing import Generator
from queue import Queue
class Scheduler:
def __init__(self):
self.ready = Queue()
self.task_map = {}
def add_task(self, coroutine: Generator) -> int:
new_task = Task(coroutine)
self.task_map[new_task.tid] = new_task
self.schedule(new_task)
return new_task.tid
def exit(self, task: Task):
del self.task_map[task.tid]
def schedule(self, task: Task):
self.ready.put(task)
def _run_once(self):
task = self.ready.get()
try:
result = task.run()
except StopIteration:
self.exit(task)
return
self.schedule(task)
def event_loop(self):
while self.task_map:
self._run_once()
Вся работа происходит в функции event_loop(), которая просто достаёт задачи одну за другой. В функции _run_once() идёт обработка итерации цикла событий, в которой поочерёдно берутся и запускаются задачи для обработки. Если задача не завершилась, то она ставится заново в очередь задач self.ready. Выполненные задачи нужно убрать из планировщика функцией exit().
Для добавления задачи используйте функцию add_task(). Она принимает корутину для выполнения и создаёт с ней задачу в планировщике. Чтобы поставить задачу напрямую в планировщик, необходимо вызвать функцию schedule().
Далее разберёмся с устройством задачи.
import types
from typing import Generator, Union
class Task:
task_id = 0
def __init__(self, target: Generator):
Task.task_id += 1
self.tid = Task.task_id # Task ID
self.target = target # Target coroutine
self.sendval = None # Value to send
self.stack = [] # Call stack
# Run a task until it hits the next yield statement
def run(self):
while True:
try:
result = self.target.send(self.sendval)
if isinstance(result, types.GeneratorType):
self.stack.append(self.target)
self.sendval = None
self.target = result
else:
if not self.stack:
return
self.sendval = result
self.target = self.stack.pop()
except StopIteration:
if not self.stack:
raise
self.sendval = None
self.target = self.stack.pop()
Сама по себе задача — обёртка над корутиной. У каждой задачи есть свой id, который учитывается в планировщике в словаре task_map. На его заполненность смотрит планировщик при выполнении задач.
Другая особенность задач — возможность выполнения корутин методом run(). Давайте посмотрим, как они выполняются в рамках задачи. Предположим, что есть корутина, которая вызывает другую корутину, а та — третью. Например, вот такой код:
def double(x):
yield x * x
def add(x, y):
yield from double(x + y)
def main():
result = yield add(1, 2)
print(result)
yield
Код является небольшой модификацией кода Бизли из его выступления. Теперь попробуем выполнить эту цепочку корутин в рамках Task.
task = Task(main())
task.run()
9
Таким же образом будут выполняться и остальные корутины в рамках планировщика. Осталось только расширить планировщик для работы с I/O-операциями.
В рамках планировщика добавляем специальную бесконечную задачу io_task перед стартом цикла событий. Эта функция имеет бесконечный цикл внутри и передаёт управление планировщику после вызова выполненных событий из селектора.
import logging
from typing import Generator, Union
from queue import Queue
from selectors import DefaultSelector, EVENT_READ, EVENT_WRITE
logger = logging.getLogger(__name__)
class Scheduler:
def __init__(self):
self.ready = Queue()
self.selector = DefaultSelector()
self.task_map = {}
def add_task(self, coroutine: Generator) -> int:
new_task = Task(coroutine)
self.task_map[new_task.tid] = new_task
self.schedule(new_task)
return new_task.tid
def exit(self, task: Task):
logger.info('Task %d terminated', task.tid)
del self.task_map[task.tid]
# I/O waiting
def wait_for_read(self, task: Task, fd: int):
try:
key = self.selector.get_key(fd)
except KeyError:
self.selector.register(fd, EVENT_READ, (task, None))
else:
mask, (reader, writer) = key.events, key.data
self.selector.modify(fd, mask | EVENT_READ, (task, writer))
def wait_for_write(self, task: Task, fd: int):
try:
key = self.selector.get_key(fd)
except KeyError:
self.selector.register(fd, EVENT_WRITE, (None, task))
else:
mask, (reader, writer) = key.events, key.data
self.selector.modify(fd, mask | EVENT_WRITE, (reader, task))
def _remove_reader(self, fd: int):
try:
key = self.selector.get_key(fd)
except KeyError:
pass
else:
mask, (reader, writer) = key.events, key.data
mask &= ~EVENT_READ
if not mask:
self.selector.unregister(fd)
else:
self.selector.modify(fd, mask, (None, writer))
def _remove_writer(self, fd: int):
try:
key = self.selector.get_key(fd)
except KeyError:
pass
else:
mask, (reader, writer) = key.events, key.data
mask &= ~EVENT_WRITE
if not mask:
self.selector.unregister(fd)
else:
self.selector.modify(fd, mask, (reader, None))
def io_poll(self, timeout: Union[None, float]):
events = self.selector.select(timeout)
for key, mask in events:
fileobj, (reader, writer) = key.fileobj, key.data
if mask & EVENT_READ and reader is not None:
self.schedule(reader)
self._remove_reader(fileobj)
if mask & EVENT_WRITE and writer is not None:
self.schedule(writer)
self._remove_writer(fileobj)
def io_task(self) -> Generator:
while True:
if self.ready.empty():
self.io_poll(None)
else:
self.io_poll(0)
yield
def schedule(self, task: Task):
self.ready.put(task)
def _run_once(self):
task = self.ready.get()
try:
result = task.run()
except StopIteration:
self.exit(task)
return
self.schedule(task)
def event_loop(self):
self.add_task(self.io_task())
while self.task_map:
self._run_once()
Код значительно разросся, но на самом деле ничего страшного не произошло. Рассмотрим изменения в порядке вызовов. В рамках планировщика добавляем специальную бесконечную задачу io_task перед стартом цикла событий. Эта функция имеет бесконечный цикл внутри и передаёт управление планировщику после вызова выполненных событий из селектора.
Рассмотрим подробнее устройство io_task. Если очередь задач пустая, то timeout для ожидания событий из селектора ставится в режим «до тех пор, пока не будет новых событий». В остальных случаях ставим таймаут 0, чтобы получить все события от ОС сразу же. Такую особенность работы этого метода рассмотрим чуть позже.
Если из селектора пришли новые события, то обрабатываем их и убираем из обработки файловые дескрипторы. Важный момент — хранение данных о задачах в селекторе. Одна и та же задача может ожидать чтения данных и пытаться записать новые данные. Именно поэтому в поле data хранится кортеж (reader, writer).
По сути, event_loop должен предоставлять интерфейс для работы с сокетами. Таких метода всего четыре:
wait_for_read,wait_for_write,_remove_reader,_remove_writer.
Эти методы позволяют работать с циклом событий, встроенным в ОС.
Работа с I/O для цикла событий — «пристройка сбоку» для обработки сетевых запросов. То есть основное назначение цикла событий в Python — обработка функций корутин, которые могут никуда не ходить по сети, а работать только с файловой системой.
Осталось разобраться с конструкцией SystemCall. Так как изначально цикл событий больше напоминает работу ОС, должен быть механизм прерываний, чтобы передать управление ОС. В асинхронном коде прерывание обеспечивается с помощью yield. После переключения контекста может вызываться системная функция для исполнения. Например, для создания новых задач можно использовать вот такой код:
class SystemCall:
def handle(self, sched: Scheduler, task: Task):
pass
class NewTask(SystemCall):
def __init__(self, target: Generator):
self.target = target
def handle(self, sched: Scheduler, task: Task):
tid = sched.add_task(self.target)
task.sendval = tid
sched.schedule(task)
В Scheduler достаточно добавить небольшой фрагмент кода:
class Scheduler:
...
def _run_once(self):
task = self.ready.get()
try:
result = task.run()
if isinstance(result, SystemCall):
result.handle(self, task)
return
except StopIteration:
self.exit(task)
return
self.schedule(task)
А в Task добавляем небольшое условие при выполнении корутин:
import types
from typing import Generator, Union
class Task:
...
def run(self):
while True:
try:
result = self.target.send(self.sendval)
if isinstance(result, SystemCall):
return result
...
Что всё это значит? Разберёмся на примере NewTask. Этот класс предоставляет интерфейс для создания новых задач в цикле событий. Такой интерфейс позволяет абстрагировать клиентский код. Это эмуляция защищённой среды ОС, когда последняя предоставляет безопасные методы для работы с ядром. Такие методы не дают клиентскому коду мешать другим программам в ОС. Таким же образом можно сделать KillTask или WaitTask.
Осталась последняя проблема — блокирующие операции. Из-за них код не может асинхронно обрабатывать события и цикл событий ждёт выполнения на каждой функции. Есть вариант решения проблемы:
- Сделать неблокирующими сокеты через
socket.setblocking(False).
Asyncio
Теперь у нас достаточно знаний, чтобы без труда освоить основную встроенную библиотеку для асинхронного программирования — asyncio.
С версии Python 3.5 в язык добавили специальный синтаксис — async/await. Он позволяет использовать «нативные» корутины, которые теперь являются частью языка. Они разделяют генераторы от асинхронного кода, что позволяет создавать асинхронные генераторы и ускорять работу асинхронного кода.
Посмотрим, как выглядит простая программа с использованием async/await.
import random
import asyncio
async def func():
r = random.random()
await asyncio.sleep(r)
return r
async def value():
result = await func()
print(result)
if __name__ == '__main__':
loop = asyncio.get_event_loop()
loop.run_until_complete(value())
loop.close()
В целом изменений немного. Переменная loop — это не что иное, как планировщик задач. Он работает по схожим принципам с тем, что рассматривался ранее. Теперь все функции переключаются с помощью await.
Познакомимся с основными функциями asyncio, которые часто встречаются на практике:
gather— выполняет список корутин одновременно и дожидается результата выполнения всех корутин.sleep— заставляет корутину уснуть на определённое количество секунд.wait/wait_for— удобные функции, чтобы дождаться выполнения уже запущенной корутины.
Также стоит ознакомиться с основными функциями event_loop:
get_event_loop— получить новый объектevent_loopили тот, что уже существует. При этом одновременно может существовать только один объектevent_loop.run_until_complete/run— удобные функции для запуска и проверки асинхронных функций.shutdown_asyncgens— одна из самых недооценённых функций цикла событий, которая позволяет правильно завершить выполнение цикла событий и всех корутин.call_soon— позволяет запланировать выполнение корутины, но не ждать её выполнения. Таким образом можно вечно ставить на выполнение одну и ту же функцию.
Теперь стоит поговорить про ключевые различия между asyncio и предложенной реализацией цикла событий. Asyncio работает на функциях обратного вызова или колбэках (callback). Этот механизм запускает задачи «честнее», чем текущий планировщик. Каждая корутина по-честному ставится в очередь и исполняется. В простом планировщике переключения не произойдёт, пока вся цепочка корутин не выполнится, что блокирует выполнение остальных задач. Однако, у колбэков есть и свой недостаток — callback hell. Это состояние, когда после вызова каждой функции нужно вызвать ещё одну функцию и ещё одну функцию... Получаются интересные фрагменты кода:
func1.add_callback(
func2.add_callback(
func3.add_callback(func4)
)
)
К счастью, этого удаётся избежать через синтаксис async/await.
await func4()
await func3()
await func2()
await func1()
Такое поведение возможно благодаря введению класса Future. По сути, такие объекты спасают от колбэков и делают код более линейным. В современных версиях Python Future-объекты для нативных корутин не нужны.
Коды и скрипты
Уравнение огибающей Капчинского-Владимирского для пучка заряженных частиц
Сначала разберем теорию, а затем расчитаем огибающую электронного пучка в линейном ускорителе с помощью Python.
Уравнения Максвелла
Объемная плотность тока пучка \(\jmath = \rho\upsilon\), где \(\rho\) - объемная плотность заряда, \(\upsilon\) - скорость пучка. Запишем дифференциальные уравнения Максвелла: $$ \nabla \vec{D} = 4\pi\rho, $$ $$ \nabla\times \vec{H} = \frac{4\pi\vec{\jmath}}{c}, $$ где \(\vec{D}\) - индукция электрического поля, \(\vec{H}\) - напряженность магнитного поля, \(с\) - скорость света. Используем теорему Стокса об интегрировании дифференциальных форм, чтобы получить уравнения Максвелла в интегральной форме: $$ \oint\limits_{\eth V} \vec{D}\vec{dS} = 4\pi\int\limits_V\rho{dV}, $$ $$ \oint\limits_{\eth S} \vec{H}\vec{dl} = \frac{4\pi}{c}\int\limits_S\vec{\jmath}\vec{dS}. $$
Найдем \(D_r\) для цилиндрического пучка радиуса \(a\) с постоянной плотностью \(\rho_0\): $$ D_r = \frac{4\pi}{r}\int\limits^r_0\rho(\xi)\xi d\xi = \begin{equation*} \begin{cases} \displaystyle 2\pi\rho_0 r, r < a, \ \displaystyle \frac{2\pi\rho_0 a^2}{r}, r > a. \end{cases} \end{equation*} $$
Учитывая, что в вакууме \(D = E\), \(H = B\), \(E\) - напряженность электрического поля, \(B\) - индукция магнитного поля, и в плоском пространстве в декартовой системе координат \(H_\alpha = \beta D_r\), где \(\displaystyle\beta = \frac{\upsilon}{c}\), радиальная компонента силы \(F_r\) из силы Лоренца \(\vec{F} = e\vec{E} + \displaystyle\frac{e}{c}\vec{\upsilon}\times\vec{B}\) : $$ F_r = eE_r - \frac{e\upsilon_z B_\alpha}{c} = eE_r(1-\displaystyle \frac{\upsilon^2}{c^2}) = \displaystyle \frac{eE_r}{\gamma^2}. $$ Полезно выразить поле через ток $$ I = \rho_0\upsilon\pi a^2, $$ тогда: $$ E_r = \begin{equation*} \begin{cases} \displaystyle \frac{2 I r}{a^2\upsilon}, r < a, \ \displaystyle \frac{2 I}{r\upsilon}, r > a. \end{cases} \end{equation*} $$
Уравнения движения
Второй закон Ньютона \(\dot p_r = F_r\), используем параксиальное приближение и считаем \(\gamma = const\): $$ \gamma m \ddot r = \displaystyle \frac{eE_r}{\gamma^2} = \displaystyle \frac{2 I e}{\gamma^2 a^2 \upsilon} r, $$ получилось линейное уравнение, но так как все частицы движутся нужно учесть, что \(a = a(t)\). Решение линейного уравнения можно представить как линейное преобразование фазовой плоскости. Так как отрезок на фазовой плоскости при невырожденном линейном преобразовании переходит в отрезок, то его можно охарактеризовать одной точкой. Следовательно, выберем крайнюю точку \(r = a\), которая будет характеризовать крайнюю траекторию: $$ \gamma m \ddot r = \displaystyle \frac{2 I e}{\gamma^2 a \upsilon}. $$ Перейдем к дифференцированию по \(z\), учтем, что \(\displaystyle dt = \frac{dz}{v}\), тогда: $$ a'' = \displaystyle \frac{e}{a}\frac{2I}{m\gamma^3\upsilon^3}. $$ Введем характерный альфвеновский ток \(I_a = \displaystyle \frac{mc^3}{e} \approx\) 17 kA, следовательно: $$ a'' = \displaystyle \frac{2I}{I_a (\beta\gamma)^3} \frac{1}{a}. $$ Учтем внешнюю фокусировку, предполагая суперпозицию полей (верно не всегда, например, в нелинейных средах это не выполняется), получим: $$ a'' + k(z)a - \displaystyle \frac{2I}{I_a (\beta\gamma)^3} \frac{1}{a} = 0, $$ что напоминает уравнение огибающей: $$ w'' + kw - \displaystyle \frac{1}{w^3} = 0 ,$$ где \( w =\displaystyle \sqrt \beta .\)
Уравнения огибающей для эллиптического пучка с распределением Капчинского-Владимирского с внешней фокусировкой линейными полями
Распределение Капчинского-Владимирского: $$ f = A\delta(1 - \displaystyle\frac{\beta_x x'^2 + 2\alpha_x x x' + \gamma_x x^2}{\epsilon_x} - \displaystyle\frac{\beta_y y'^2 + 2\alpha_y y y' + \gamma_y y^2}{\epsilon_y} ), $$ где \(А\) - инвариант Куранта-Снайдера. Полуоси эллипса: $$ a = \sqrt{\epsilon_x \beta_x}, b = \sqrt{\epsilon_y \beta_y}. $$ Поле получается линейно внутри заряженного эллиптического цилиндра: $$ E_x = \displaystyle \frac{4I}{\upsilon}\frac{x}{a(a+b)}, $$ $$ E_y = \displaystyle \frac{4I}{\upsilon}\frac{y}{b(a+b)}. $$ Проверим, что \(\nabla \vec{E} = 4\pi\rho:\) $$ \displaystyle I = \rho \upsilon \pi ab, $$ $$ \nabla \vec{E} = \displaystyle \frac{4I(a+b)}{\pi(a+b)ab} = \displaystyle \frac{4I}{\pi ab} = 4\pi\rho. $$ Так как поля линейные, они добавятся к полям фокусирующей линзы. Подставим в уравнение огибающей \(\displaystyle a = \sqrt \epsilon_x w_x, b = \sqrt \epsilon_y w_y:\) $$ a'' + k_{xt} a - \frac{\epsilon_x^2}{a^3} = 0, $$ где \(k_{xt} = k_x + k_{xsc}\) - полная жесткость, \(k_x\) - жесткость линзы, а \(\displaystyle k_{xsc} = \frac{4I}{I_a (\beta\gamma)^3}\frac{1}{a(a+b)}.\) В итоге получаем систему уравнений, связанных через пространственный заряд: $$ \begin{equation*} \begin{cases} \displaystyle a'' + k_xa - \frac{4I}{I_a (\beta\gamma)^3}\frac{1}{(a+b)} - \frac{\epsilon_x^2}{a^3} = 0 , \\ \displaystyle b'' + k_yb - \frac{4I}{I_a (\beta\gamma)^3}\frac{1}{(a+b)} - \frac{\epsilon_y^2}{b^3} = 0. \end{cases} \end{equation*} $$
Количественный критерий применимости приближения ламинарности течения
Данная система уравнений позволяет учесть 2 эффекта, мешающих сфокусировать пучок в точку - конечность эммитанса и пространственный заряд. Работают члены одинаково, поэтому можно сравнить эти величины. Когда ток \(I\) малый - слабое отталкивание, если ток \(I\) большой - сильное отталкивание, следовательно, эммитанс можно откинуть и считать течение ламинарным. Очевидно, количественный критерий применимости ламинарности течения выглядит так: $$ \displaystyle \sqrt{\frac{2I}{I_a(\beta\gamma)^3}} \gg \sqrt{\frac{\epsilon}{\beta}}. $$ Видно, что пространственный заряд влияет на огибающую больше там, где \(\beta\)-функция больше, а в вблизи фокуса влиянием пространственного заряда можно пренебречь.
Теорема Буша
В качестве дополнения к выводу уравнения огибающей пучка докажем важную вспомогательную теорему, которая называется теоремой Буша. Она связывает угловую скорость заряженной частицы, движущейся в аксиально-симметричном магнитном поле, с магнитным потоком, охваченным окружностью с центром на оси и проходящим через точку, в которой расположена частица.
Рассмотрим заряд \(q\), движущийся в магнитном поле \(\vec B = (B_r,0,B_z)\). Приравняем \(\theta\) - составляющую силы Лоренца к производной момента импульса по времени, деленной на \(r\): $$ F_\theta = -q(\ddot r B_z - \dot z B_r) = \frac{d}{rdt}(\gamma m r^2 \dot \theta). $$ Поток, пронизывающий площадь, охваченную окружностью радиуса $r$, центр которой расположен на оси, а сама она проходит через точку, в которой расположен заряд, записывается в виде \(\psi = \int\limits^r_0 2\pi r B_z dr\). Когда частица перемещается на \(\vec{dl} = (dr,dz)\), скорость изменения потока, охваченного этой окружностью, можно найти из второго уравнения Максвелла \(\nabla \vec{B} = 0.\) Таким образом, $$ \dot\psi = 2\pi r (-B_r \dot z + B_z \dot r). $$ После интегрирования по времени из приведенных уравнений получаем следующее выражение: $$ \dot \theta = (-\frac{q}{2\pi \gamma m r^2})(\psi - \psi_0). $$
Уравнение параксиального луча
Здесь мы запишем уравнение параксиального луча в виде, соответсвующем системе с аксиальнорй симметрией при принятых ранее допущениях. Чтобы вывести уравнение параксиального луча, приравняем силу радиального ускорения силам электрическим и магнитным со стороны внешних полей. Нужно помнить, что величина \(\gamma = \gamma(t).\) $$ \frac{d}{dt}(\gamma m \dot r) - \gamma m r (\dot \theta)^2 = q(E_r + r\dot \theta B_z). $$ Применим теорему Буша и независимость \(B_z\) от \(r:\) $$ -\dot \theta = \frac{q}{2\gamma m}(B_z - \frac{\psi_0}{\pi r}). $$ Исключим $\dot \theta$ и подставим $\displaystyle \dot \gamma \approx \frac {\beta q E_z }{mc}:$ $$ \ddot r + \frac{\beta q E_z}{\gamma m c} \dot r + \frac{q^2 B^2_z}{4\gamma ^2 m^2} r - \frac{ q^2 \psi^2_0}{4\pi^2\gamma^2 m^2} (\frac{1}{r^3}) - \frac{q E_r}{\gamma m } = 0. $$
Уравнение огибающей для круглого и эллиптического пучка
Учитывая, что: $$ \dot r = \beta c r', $$ $$ \ddot r = r'' (\dot z)^2 + r'\ddot z \approx r'' \beta^2 c^2 + r' \beta' \beta c^2. $$ А также, если в области пучка нет никаких зарядов, то, разлагая в ряд Тейлора в окрестности оси и оставляя только первый член, с учетом $$\nabla \vec{E} = 0$$ получаем $$ E_r = -0.5 r E'_z \approx - 0.5 r \gamma'' mc^2/q. $$ Тогда окончательно можем записать уравнение огибающей для круглого пучка радиуса \(r\) с распределением Капчинского-Владимирского с внешней фокусировкой линейными полями: $$ \displaystyle r'' + \frac{1}{\beta^2\gamma} \gamma' r' + \frac{1}{2\beta^2\gamma}\gamma''r + kr - \frac{2I}{I_a (\beta\gamma)^3}\frac{1}{r} - \frac{\epsilon^2}{r^3} = 0 ; $$ и для эллиптического пучка: $$ \begin{equation*} \begin{cases} \displaystyle a'' + \frac{1}{\beta^2\gamma} \gamma' a' + \frac{1}{2\beta^2\gamma}\gamma''a + k_xa - \frac{4I}{I_a (\beta\gamma)^3}\frac{1}{(a+b)} - \frac{\epsilon_x^2}{a^3} = 0 , \\ \displaystyle b'' + \frac{1}{\beta^2\gamma} \gamma' b' + \frac{1}{2\beta^2\gamma}\gamma''b + k_yb - \frac{4I}{I_a (\beta\gamma)^3}\frac{1}{(a+b)} - \frac{\epsilon_y^2}{b^3} = 0. \end{cases} \end{equation*} $$
Магнитные линзы
Фокусирующими элементами могут являться: соленоиды и магнитные квадрупольные линзы.
Соленоиды
\(k_x = k_y = k_s\) - жесткость соленоида: $$ k_s = \left ( \frac{eB_z}{2m_ec\beta\gamma} \right )^2 = \left ( \frac{e B_z}{2\beta\gamma\cdot 0.511\cdot 10^6 e \cdot \mathrm{volt}/c} \right )^2 = \left ( \frac{cB_z[\mathrm{T}]}{2\beta\gamma\cdot 0.511\cdot 10^6 \cdot \mathrm{volt}} \right )^2. $$
Квадруполи
\(k_q = \displaystyle\frac{eG}{pc}\) - жесткость квадруполя, где \(G = \displaystyle\frac{\partial B_x}{\partial y} = \displaystyle\frac{\partial B_y}{\partial x}\) - градиент магнитного поля, причем \(k_x = k_q, k_y = -k_q.\) $$ k_q = \left ( \frac{eG}{m_ec\beta\gamma} \right ) = \left ( \frac{eG}{\beta\gamma\cdot 0.511\cdot 10^6 e \cdot \mathrm{volt}/c} \right ) = \left ( \frac{cG}{\beta\gamma\cdot 0.511\cdot 10^6 \cdot \mathrm{volt}} \right ). $$
Продольная динамика пучка
Уравнение на продольную динамику пучка можно решить независимо от уравнения на огибающую, чтобы в уравнении на огибающую уже использовать готовую функцию энергии пучка от \(z\). Считая, что скорость электрона достаточно близка к скорости света и следовательно его продольная координата \(z \approx ct\), а импульс \(p_z \approx \gamma mc\)
$$ \frac{d\gamma}{dz} \approx \frac{eE_z}{mc^2}, $$
Тогда достаточно один раз проинтегрировать функцию \(E_z(z)\):
Решение уравнения огибающей для эллиптического пучка с фокусирующими элементами
Уравнение огибающей для эллиптического пучка с полуосями \(a, b\) с распределением Капчинского-Владимирского с внешней фокусировкой линейными полями: $$ \begin{equation*} \begin{cases} \displaystyle a'' + \frac{1}{\beta^2\gamma} \gamma' a' + \frac{1}{2\beta^2\gamma}\gamma''a + k_qa - \frac{2P}{(a+b)} - \frac{\epsilon_x^2}{a^3} = 0 , \\ \displaystyle b'' + \frac{1}{\beta^2\gamma} \gamma' b' + \frac{1}{2\beta^2\gamma}\gamma''b - k_qb - \frac{2P}{(a+b)} - \frac{\epsilon_y^2}{b^3} = 0. \end{cases} \end{equation*} $$
Пусть \(\displaystyle x = \frac{da}{dz}, y = \frac{db}{dz}, \displaystyle \frac{d\gamma }{dz}\approx \frac{e E_z}{m c^2}, k = \frac{1}{R} - \) кривизна, тогда $$ \begin{matrix} \displaystyle \frac{dx}{dz}= - \frac{1}{\beta^2\gamma} \gamma' a' - \frac{1}{2\beta^2\gamma}\gamma''a - k_qa + \frac{2P}{(a+b)} + \frac{\epsilon_x^2}{a^3}\\ \displaystyle\frac{da}{dz} = x\\ \displaystyle \frac{dy}{dz}= - \frac{1}{\beta^2\gamma} \gamma' b' - \frac{1}{2\beta^2\gamma}\gamma''b + k_qb + \frac{2P}{(a+b)} + \frac{\epsilon_x^2}{b^3}\\ \displaystyle\frac{db}{dz} = y \end{matrix}. $$ Пусть \(\vec X = \begin{bmatrix} x \\ a \\ y \\ b \end{bmatrix} \), теперь составим дифференциальное уравнение \(X' = F(X).\)
Уравнение траектории для одной частицы
Векторный потенциал в соленоиде имеет только одну компоненту и легко выражается через \(B_z(z)\): $$ A_\phi (z,r)=\sum_0^{inf} \dfrac{(-1)^n}{n!(n+1)!} B_z^{2n}(\dfrac{r}{2})^{2n+1/2}. $$ Следовательно Лагранжиан в цилиндрической системе координат имеет вид: $$ L = -mc^2(1-\beta^2)^{1/2} + \dfrac{e}{c}A_\phi r \dot\phi. $$ Из аксиальной симметрии следует существование интеграла движения: $$ P_\phi = \gamma mr^2\dot\phi + \dfrac{e}{c} r A_\phi = \gamma mr^2\dot\phi_0. $$ Продифференцировав по $z$ получим: $$ \phi' - \phi_0' = -\dfrac{e}{pc}\dfrac{A_\phi}{r}. $$ И в параксиальном приближении: $$ \phi' - \phi_0' = -\dfrac{e}{pc}B_z(z). $$ Откуда: $$ \delta \phi = \int\dfrac{e}{2pc}B_z(z)dz. $$ Тогда и уравнения траектории в приведенных координатах выглядят так: $$ \begin{equation*} \begin{cases} \displaystyle \tilde x'' + \frac{1}{\beta^2\gamma} \gamma'\tilde x' + \frac{1}{2\beta^2\gamma}\gamma''\tilde x + k_s \tilde x = 0 , \\ \displaystyle \tilde y'' + \frac{1}{\beta^2\gamma} \gamma'\tilde y' + \frac{1}{2\beta^2\gamma}\gamma''\tilde y +k_s \tilde y = 0, \end{cases} \end{equation*} $$
Расчет в Python
Сначала подключим необходимые библиотеки и настроим параметры графики
import numpy as np
import holoviews as hv
hv.extension('matplotlib')
%output size=200 backend='matplotlib' fig='svg'
%opts Curve Scatter Area [fontsize={'title':14, 'xlabel':14, 'ylabel':14, 'ticks':14, 'legend': 14}]
%opts Area Curve [aspect=3 show_grid=True]
%opts Area (linewidth=1 alpha=0.25)
%opts Curve (linewidth=2 alpha=0.5)
import warnings
warnings.filterwarnings('ignore')
Настроим область и шаг счета
dz = 0.005 # m
z_min = 0.7
z_max = 15
z = np.arange(z_min,z_max,dz) # m
Определим элемент ускорителя (напр. соленоид, или ускоряющий зазор). Ускоритель будем представлять в виде последовательности таких элементов.
class Element:
def __init__(self, z0, MaxField, filename, name):
self.z0 = z0
self.MaxField = MaxField
self.filename = filename
self.name = name
Фокусирующие соленоиды:
Bz_beamline = {}
for z0, B0, filename, name in [
# m T Unique name
[ 0.95, 0.001, 'input/fields/B_z(z).dat', 'Sol. 1' ],
[ 2.1, 0.03, 'input/fields/B_z(z).dat', 'Sol. 2' ],
[ 2.9077, 0.001, 'input/fields/B_z(z).dat', 'Sol. 3' ],
[ 4.0024, 0.03, 'input/fields/B_z(z).dat', 'Sol. 4' ],
[ 5.642, 0.03, 'input/fields/B_z(z).dat', 'Sol. 5' ],
[ 6.760, 0.001, 'input/fields/B_z(z).dat', 'Sol. 6' ],
]:
Bz_beamline[name] = Element(z0, B0, filename, name)
Bz_beamline['Sol. 3'].z0
2.9077
Ускоряющие элементы:
Ez_beamline = {}
for z0, E0, filename, name in [
# m MV/m Unique name
[ 7.456, -0.9, 'input/fields/E_z(z).dat', 'Cavity 3'],
[ 8.838, -0.9, 'input/fields/E_z(z).dat', 'Cavity 4'],
[ 10.220, -0.9, 'input/fields/E_z(z).dat', 'Cavity 5'],
[ 11.602, -0.9, 'input/fields/E_z(z).dat', 'Cavity 6'],
[ 12.984, -0.9, 'input/fields/E_z(z).dat', 'Cavity 7'],
[ 14.366, -0.9, 'input/fields/E_z(z).dat', 'Cavity 8'],
]:
Ez_beamline[name] = Element(z0, E0, filename, name)
Считывание профилей фокусирующего и ускоряющего поля
Сперва мы просто считываем поля из файлов и сшиваем их в один массив:
from scipy import interpolate
FieldFiles = {} # buffer for field files
def read_field(beamline, z):
global FieldFiles
F = 0
for element in beamline.values():
if not (element.filename in FieldFiles):
print('Reading ' + element.filename)
FieldFiles[element.filename] = np.loadtxt(element.filename)
M = FieldFiles[element.filename]
z_data = M[:,0]
F_data = M[:,1]
f = interpolate.interp1d(
element.z0+z_data, element.MaxField*F_data,
fill_value=(0, 0), bounds_error=False
)
F = F + f(z)
return F
Bz = read_field(Bz_beamline, z)
Reading input/fields/B_z(z).dat
Для интегрирования уравнения на огибающую необходимо сконвертировать массив Bz в функцию Bz(z)
Bz = interpolate.interp1d(z, Bz, fill_value=(0, 0), bounds_error=False)
Теперь Bz уже функция, которая быстро может вывести поле в любых точках вдоль ускорителя.
Bz(2.11111)
array(0.02984419)
Построим поле \(Bz(z)\)
dim_z = hv.Dimension('z', unit='m', range=(0,z_max))
dim_Bz = hv.Dimension('Bz', unit='T', label='$B_z$')
z_Bz = hv.Area((z,Bz(z)), kdims=dim_z, vdims=dim_Bz)
z_Bz
Аналогично для ускоряющего электрического поля:
Ez = 1*read_field(Ez_beamline, z)
Ez = interpolate.interp1d(z, Ez, fill_value=(0, 0), bounds_error=False)
dim_Ez = hv.Dimension('Ez', unit='MV/m', label=r'$E_z$')
z_Ez = hv.Area((z,Ez(z)), kdims=dim_z, vdims=dim_Ez)
z_Ez
Продольная динамика пучка
Уравнение на продольную динамику пучка можно решить независимо от уравнения на огибающую, чтобы в уравнении на огибающую уже использовать готовую функцию энергии пучка от \(z\). Считая, что скорость электрона достаточно близка к скорости света и следовательно его продольная координата \(z \approx ct\), а импульс \(p_z \approx \gamma mc\)
$$ \frac{d\gamma}{dz} \approx \frac{eE_z}{mc^2}, $$
Тогда достаточно один раз проинтегрировать функцию \(E_z(z)\):
mc = 0.511 # MeV/c
#p_z = 2.459 # MeV/c
E_0 = 2.000 # MeV
gamma_0 = E_0/mc + 1 # Начальный релятивистский фактор пучка
#gamma_0 = p_z/mc
from scipy import integrate
gamma = gamma_0 + integrate.cumtrapz(-Ez(z)/mc, z)
dim_gamma = hv.Dimension('gamma', label=r'$\gamma$', range=(0,None))
z_gamma = hv.Curve((z,gamma), kdims=dim_z, vdims=dim_gamma)
(z_gamma + z_Ez).cols(1)
Для дальнейшего использования в решении уравнения на огибающую преобразуем массив gamma в функцию:
gamma = interpolate.interp1d(z[1:], gamma, fill_value=(gamma[0], gamma[-1]), bounds_error=False)
#hv.Curve((z,gamma(z)), kdims=dim_z, vdims=dim_gamma)
Решение уравнения огибающей для круглого пучка
Уравнение огибающей для круглого пучка радиуса \(r\) с распределением Капчинского-Владимирского с внешней фокусировкой линейными полями: $$ \displaystyle r'' + \frac{1}{\beta^2\gamma} \gamma' r' + \frac{1}{2\beta^2\gamma}\gamma''r + kr - \frac{2I}{I_a (\beta\gamma)^3}\frac{1}{r} - \frac{\epsilon^2}{r^3} = 0. $$
Перейдем к среднеквадратичному радиусу для распределения Капчинского-Владимирского и перевеансу \(\displaystyle r_{rms} = \frac{r}{2}\) и \(\displaystyle P = \frac{2I}{I_a\beta^3\gamma^3} \). Получим $$ \displaystyle r_{rms}'' + \frac{1}{\beta^2\gamma} \gamma' r_{rms}' + \frac{1}{2\beta^2\gamma}\gamma''r_{rms} + kr_{rms} - \frac{P}{4r_{rms}} - \frac{\epsilon^2}{16{r_{rms}}^3} = 0. $$
Пусть \(\displaystyle y=\frac{dr_{rms}}{dz}, \displaystyle \frac{d\gamma }{dz}\approx \frac{e E_z}{m c^2}\), тогда $$ \begin{matrix} \displaystyle \frac{dy}{dz}= - \frac{1}{\beta^2\gamma} \gamma' r_{rms}' - \frac{1}{2\beta^2\gamma}\gamma''r_{rms} - kr_{rms} + \frac{P}{4r_{rms}} + \frac{\epsilon^2}{16r_{rms}^3}\\ \displaystyle\frac{dr_{rms}}{dz} = y \end{matrix}. $$ Пусть \(\vec X = \begin{bmatrix} y \ r_{rms} \ \end{bmatrix} \), теперь составим дифференциальное уравнение \(X' = F(X).\)
\(k\) - жесткость соленоида:$$ k = \left ( \frac{eB_z}{2m_ec\beta\gamma} \right )^2 = \left ( \frac{e B_z}{2\beta\gamma\cdot 0.511\cdot 10^6 e \cdot \mathrm{volt}/c} \right )^2 = \left ( \frac{cB_z[\mathrm{T}]}{2\beta\gamma\cdot 0.511\cdot 10^6 \cdot \mathrm{volt}} \right )^2. $$
c = 299792458 # (m/s) скорость света
Зададим начальные условия
I = 2000#2000.000 # A Ток в ускорителе
Ia = 17000 # A Альфвеновский ток
emitt_n = 1.80e-4#1.80e-5 # m нормализованный эммитанс
R_rms = 27.5e-3 #m r_rms пучка
dR_rmsdz = 35.4e-3 #50e-3 dr_rms/dz пучка ## 50/2*sqrt(2) = 35.4
from scipy.integrate import odeint
from scipy.misc import derivative
def dXdz(X, z):
y = X[0]
sigma = X[1]
g = gamma(z)
dgdz = Ez(z)/mc
d2gdz2 = derivative(lambda z:Ez(z),z, dz)/mc
beta = np.sqrt(1-1/(g*g))
K = ( c * Bz(z) / (2*0.511e6))**2
emitt = emitt_n/(g*beta) # m
P=2*I/(Ia*beta*beta*beta*g*g*g)
dydz = P/(4*sigma) + emitt*emitt/(sigma*sigma*sigma*16) - K*sigma/(g*beta)**2 - \
dgdz*y/(beta*beta*g) - d2gdz2*sigma/(2*beta*beta*g)
dsigmadz = y
return [dydz, dsigmadz]
Функция решения уравнения на огибающую пучка:
def find_sigma(z):
X0 = [dR_rmsdz, R_rms]
sol = odeint(dXdz, X0, z, rtol = 0.001) # rtol - относительная точность (по умолчанию rtol = 1.49012e-8)
sigma = sol[:, 1] # m
return sigma # m
%opts Area.Beam [aspect=3 show_grid=True] (color='red' linewidth=1 alpha=0.3)
sigma = find_sigma(z)
dim_sig = hv.Dimension('r_{rms}', label="$r_{rms}$", unit='mm', range=(0,150))
sigma_img = hv.Area((z,sigma*1e3), kdims=[dim_z], vdims=[dim_sig], group='Beam')
sigma_img
Релятивисткая разностная схема для расчета динамики частиц в сложных электрических и магнитных полях
First, we write the main quantities in the difference scheme, then we consider the algorithm.
Basic values
At the initial time \(t\) set Cartesian coordinates of the \(i -\)particles \(\overrightarrow{r_{i}} = (x_i, y_i, z_i)\)nd the initial pulses \(\overrightarrow{p_{i}} = (p_{x_i}, p_{y_i}, p_{z_i})\). Minimum time step is set \(\delta t\).
For convenience, made dimensionless physical quantities (with tilde): \begin{equation} \widetilde{\overrightarrow{r_i}} = \frac{\overrightarrow{r_i}}{c \delta t}, \end{equation} \begin{equation} \widetilde{\overrightarrow{E_i}} = \frac{\overrightarrow{E_i}e}{mc} \delta t, \end{equation} \begin{equation} \widetilde{\overrightarrow{H_i}} = \frac{\overrightarrow{H_i}e}{mc} \delta t, \end{equation} where \(m\) is the speed of light, \(e\) is the particle charge and \(m\) is the particle mass.
Algorithm
Consider the relativistic difference scheme algorithm step by step:
-
Calculation of electric fields \(\overrightarrow{E_i}\) at the points where the particles are.
-
Pulse increment: \begin{equation} \overrightarrow{p_i} = \overrightarrow{p_i} + 2\cdot\overrightarrow{E_i}, \end{equation} where the coefficient means that the increment of the pulse is made for the entire time interval \(2\delta t\).
-
New speeds are calculated by new impulses: \begin{equation} \overrightarrow{v_i} = \frac{\overrightarrow{p_i}}{\gamma_i}, \end{equation} where \(\gamma_i = \sqrt{1 + \overrightarrow{p_i}^2}.\)
-
At new speeds, new coordinates are calculated: \begin{equation} \overrightarrow{r_i} = \overrightarrow{r_i} + 1\cdot\overrightarrow{v_i}, \end{equation} where the coefficient means that the increment of the coordinate is made for the time interval \(\delta t.\)
-
Calculation of magnetic fields \(\overrightarrow{H_i}\) at the new points where the particles are.
-
Calculated velocity values (after rotation in a magnetic field):
\[ b_1 = 1 - \frac{H_i^2}{\gamma_i}, b_2 = 1 + \frac{H_i^2}{\gamma_i}, b_3 = 2\cdot \frac{\overrightarrow{v_i}\cdot\overrightarrow{H_i}}{\gamma_i}, \]
\[ \overrightarrow{f_i} = 2\cdot \frac{\overrightarrow{v_i}\times \overrightarrow{H_i}}{\gamma_i}, \]
\begin{equation} \overrightarrow{v_i} = \frac{\overrightarrow{v_i}b_1 + \overrightarrow{f_i} + \frac{\overrightarrow{H_i}}{\gamma_i}b_3}{b_2}. \end{equation}
-
At new speeds, new coordinates are calculated: \begin{equation} \overrightarrow{r_i} = \overrightarrow{r_i} + 1\cdot\overrightarrow{v_i}, \end{equation} where the coefficient means that the increment of the coordinate is made for the time interval $\delta t.$
-
New impulses are calculated according to the new rates: \begin{equation} \overrightarrow{p_i} = \overrightarrow{v_i}\gamma_i. \end{equation}
One cycle is performed in a time interval \(2\delta t.\)
Python
import redpic as rp
import numpy as np
import holoviews as hv
hv.extension('matplotlib')
import warnings
warnings.filterwarnings('ignore')
rp.__version__
Some plotting options
%output size=100 backend='matplotlib' fig='png' dpi=300
%opts Curve Scatter [aspect=3 show_grid=True]
%opts Curve (linewidth=1 alpha=0.7 color='blue')
%opts Scatter (alpha=0.7 s=0.5)
Define accelerator beamline parameters
acc = rp.accelerator.Accelerator(0.7, 5, 0.01)
# Unique name, z-position [m], Ez [MV/m], Ez(z) profile
acc.add_accel('Acc. 1', 4.096, -1.1, 'Ez.dat')
acc.add_accel('Acc. 2', 5.944, -1.1, 'Ez.dat')
# Unique name, z-position [m], Bz [T], Bz(z) profile
acc.add_solenoid('Sol. 1', 0.450, -0.0580, 'Bz.dat')
acc.add_solenoid('Sol. 2', 0.957, 0.0390, 'Bz.dat')
acc.add_solenoid('Sol. 3', 2.107, 0.0250, 'Bz.dat')
acc.add_solenoid('Sol. 4', 2.907, 0.0440, 'Bz.dat')
acc.add_solenoid('Sol. 5', 3.670, 0.0400, 'Bz.dat')
acc.add_solenoid('Sol. 6', 4.570, 0.0595, 'Bz.dat')
acc.add_solenoid('Sol. 7', 5.470, 0.0590, 'Bz.dat')
acc.compile()
dim_z = hv.Dimension('z', unit='m')
dim_Ez = hv.Dimension('Ez', unit='MV/m', label='$E_z$')
dim_Bz = hv.Dimension('Bz', unit='Gs', label='$B_z$')
z = acc.z
z_Ez = hv.Curve((z, acc.Ez(z)), kdims=dim_z, vdims=dim_Ez)
z_Bz = hv.Curve((z, acc.Bz(z)*1e4), kdims=dim_z, vdims=dim_Bz)
(z_Ez + z_Bz).cols(1)
print(acc)
Accelerator structure.
Solenoids:
[ 0.45 m, -0.058 T, Bz.dat, Sol. 1, 0.0 m, 0.0 rad, 0.0 m, 0.0 rad]
[ 0.957 m, 0.039 T, Bz.dat, Sol. 2, 0.0 m, 0.0 rad, 0.0 m, 0.0 rad]
[ 2.107 m, 0.025 T, Bz.dat, Sol. 3, 0.0 m, 0.0 rad, 0.0 m, 0.0 rad]
[ 2.907 m, 0.044 T, Bz.dat, Sol. 4, 0.0 m, 0.0 rad, 0.0 m, 0.0 rad]
[ 3.67 m, 0.04 T, Bz.dat, Sol. 5, 0.0 m, 0.0 rad, 0.0 m, 0.0 rad]
[ 4.57 m, 0.0595 T, Bz.dat, Sol. 6, 0.0 m, 0.0 rad, 0.0 m, 0.0 rad]
[ 5.47 m, 0.059 T, Bz.dat, Sol. 7, 0.0 m, 0.0 rad, 0.0 m, 0.0 rad]
Accelerating modules:
[ 4.096 m, -1.1 T, Ez.dat, Acc. 1, 0.0 m, 0.0 rad, 0.0 m, 0.0 rad]
[ 5.944 m, -1.1 T, Ez.dat, Acc. 2, 0.0 m, 0.0 rad, 0.0 m, 0.0 rad]
Quadrupoles:
Correctors x:
Correctors y:
Define beam parameters
beam = rp.beam.RadialUniformBeam(
type=rp.constants.electron,
energy = 1.32, # MeV
current = 0.5e3, # A
radius_x = 48e-3, # initial r (m)
radius_y = 48e-3, # initial r (m)
radius_z = 3.5,
radius_xp = 2*35.0e-3, # initial r' (rad)
radius_yp = 2*35.0e-3, # initial r' (rad)
x = 0.0e-3, # horizontal centroid position (m)
xp = 0.0e-3, # horizontal centroid angle (rad)
y = 0, # vertical centroid position (m)
normalized_emittance = 200e-6 # m*rad
)
beam.generate(10_000)
2023-08-31 21:35:33,649 - redpic.beam.base - INFO - Generate a radial-uniform beam with 10000 particles
beam.df
| x | y | z | px | py | pz | |
|---|---|---|---|---|---|---|
| 0 | 0.034491 | -0.010901 | -1.123685 | 0.100578 | -0.031122 | 1.747093 |
| 1 | 0.007980 | -0.003833 | 1.251044 | 0.022404 | -0.010670 | 1.749303 |
| 2 | -0.022694 | -0.010773 | -0.128508 | -0.067049 | -0.031592 | 1.741746 |
| 3 | 0.017086 | 0.014826 | -2.608725 | 0.048956 | 0.043029 | 1.763242 |
| 4 | -0.021815 | 0.015455 | 0.520279 | -0.062786 | 0.044937 | 1.759832 |
| ... | ... | ... | ... | ... | ... | ... |
| 9995 | 0.018885 | 0.028316 | 1.360050 | 0.054502 | 0.082155 | 1.746065 |
| 9996 | -0.021948 | 0.040885 | -2.615462 | -0.064131 | 0.119014 | 1.759089 |
| 9997 | -0.016885 | -0.017578 | 1.473440 | -0.048364 | -0.051265 | 1.740909 |
| 9998 | 0.027568 | -0.014905 | -0.467425 | 0.080297 | -0.042703 | 1.765850 |
| 9999 | 0.035333 | 0.010626 | 0.145074 | 0.103711 | 0.031025 | 1.771395 |
10000 rows × 6 columns
dim_x = hv.Dimension('x', unit='m', range=(-0.1, 0.1))
dim_y = hv.Dimension('y', unit='m', range=(-0.1, 0.1))
dim_z = hv.Dimension('z', unit='m', range=(acc.z_start, acc.z_stop))
dim_px = hv.Dimension('px', unit='MeV/c', label='$p_x$')
dim_py = hv.Dimension('py', unit='MeV/c', label='$p_y$')
beam_x_y = hv.Scatter(beam.df, kdims=[dim_x, dim_y])
beam_z_x = hv.Scatter(beam.df, kdims=[dim_z, dim_x])
beam_x_px = hv.Scatter(beam.df, kdims=[dim_x, dim_px])
beam_y_py = hv.Scatter(beam.df, kdims=[dim_y, dim_py])
WARNING:param.Scatter: Chart elements should only be supplied a single kdim
2023-08-31 21:35:33,772 - param.Scatter - WARNING - Chart elements should only be supplied a single kdim
WARNING:param.Scatter: Chart elements should only be supplied a single kdim
2023-08-31 21:35:33,789 - param.Scatter - WARNING - Chart elements should only be supplied a single kdim
WARNING:param.Scatter: Chart elements should only be supplied a single kdim
2023-08-31 21:35:33,791 - param.Scatter - WARNING - Chart elements should only be supplied a single kdim
WARNING:param.Scatter: Chart elements should only be supplied a single kdim
2023-08-31 21:35:33,801 - param.Scatter - WARNING - Chart elements should only be supplied a single kdim
(beam_x_y + beam_z_x + beam_x_px + beam_y_py).cols(2)
print(beam)
Beam parameters:
Type electron
Distribution radial-uniform
Particles 10000
Current 500.0 A
Energy 1.32 MeV
Total momentum 1.7582483378931433 MeV/c
Rel. factor 3.583175582013202
Radius x 48.0 mm
Radius y 48.0 mm
Radius z 3.5 m
Radius x prime 70.0 mrad
Radius y prime 70.0 mrad
Horizontal centroid position 0.0 mm
Vertical centroid position 0.0 mm
Horizontal centroid angle 0.0 mrad
Vertical centroid angle 0.0 mrad
Normalized emittance x 200.0 mm*mrad
Normalized emittance y 200.0 mm*mrad
Run simulation
rp_sim = rp.solver.Simulation(beam, acc)
rp_sim.track()
z = 4.98 m (99.5 %)
Plot the simulation results
def plot(i):
df = rp_sim.result[i]
rp_z_x = hv.Scatter(df, kdims=[dim_z, dim_x], label='redpic')
return rp_z_x
items = [(i, plot(i)) for i in list(rp_sim.result.keys())]
holomap = hv.HoloMap(items, kdims = ['z'])
hv.output(holomap, widget_location='bottom')
Оптимизация огибающей пучка заряженных частиц с помощью генетического алгоритма
Sometimes it’s useful to use a computer to adjust the envelope.
Genetic algorithms work similarly to natural selection in nature. The basis of the genetic algorithm is the individual, chromosomes (genes), population (set of individuals), the functions of adaptability, selection, crossing and mutation. In practice, everything happens like this: the creation of the first generation, assessment, selection, crossing, mutation, new generation, evaluation, etc. until we get the desired result.
DEAP is a framework for working with genetic algorithms, containing many ready-made tools, the main thing is to know how to use them.
Create a beam and accelerator.
import kenv as kv
beam = kv.Beam(energy=2,
current=2e3,
radius=50e-3,
rp=50e-3,
normalized_emittance=1000e-6)
accelerator = kv.Accelerator(0, 5, 0.01)
Solenoids = [
[ 0.5000, 0.02, 'Bz.dat', 'Sol. 1'],
[ 1.0000, 0.02, 'Bz.dat', 'Sol. 2'],
[ 1.5000, 0.02, 'Bz.dat', 'Sol. 3'],
[ 2.0000, 0.02, 'Bz.dat', 'Sol. 4'],
[ 2.5000, 0.02, 'Bz.dat', 'Sol. 5'],
[ 3.0000, 0.02, 'Bz.dat', 'Sol. 6'],
[ 3.5000, 0.02, 'Bz.dat', 'Sol. 7'],
[ 4.0000, 0.02, 'Bz.dat', 'Sol. 8'],
[ 4.5000, 0.02, 'Bz.dat', 'Sol. 9'],
]
for z0, B0, filename, name in Solenoids:
accelerator.Bz_beamline[name] = kv.Element(z0, B0, filename, name)
accelerator.compile()
simulation = kv.Simulation(beam, accelerator)
simulation.track()
Graphic
matplotlib
import holoviews as hv
hv.extension('matplotlib')
%opts Layout [tight=True]
%output size=150 backend='matplotlib' fig='svg'
%opts Area Curve [aspect=3 show_grid=True]
%opts Area (alpha=0.25)
%opts Curve (alpha=0.5)
%opts Area.Beam [aspect=3 show_grid=True] (color='red' alpha=0.3)
import warnings
warnings.filterwarnings('ignore')
dim_z = hv.Dimension('z', unit='m', range=(accelerator.start, accelerator.stop))
dim_Bz = hv.Dimension('Bz', unit='T', label='Bz', range=(0, 0.1))
dim_Ez = hv.Dimension('Ez', unit='MV/m', label='Ez')
dim_r = hv.Dimension('r', label="Beam r", unit='mm', range=(0, 150))
z_Bz= hv.Area((accelerator.parameter,accelerator.Bz(accelerator.parameter)), kdims=[dim_z], vdims=[dim_Bz])
z_r = hv.Area(((accelerator.parameter,simulation.envelope_x(accelerator.parameter)*1e3)), kdims=[dim_z], vdims=[dim_r], group='Beam')
(z_r+z_Bz).cols(1)
As you can see, the envelope is far from perfect.
Apply the genetic algorithm.
Genetic algorithm
First we construct a model envelope.
import numpy as np
coefficients = np.polyfit([accelerator.start, (accelerator.start+accelerator.stop)/2, accelerator.stop], [0.15, 0.05, 0.03], 2)
envelope_mod = coefficients[0]*accelerator.parameter**2 + coefficients[1]*accelerator.parameter+ coefficients[2]
z_env = hv.Curve((accelerator.parameter, envelope_mod*1e3), kdims=[dim_z], vdims=[dim_r], label='Envelope_mod', group='Beam')
z_env
Connect the necessary libraries.
import random
from deap import creator, base, tools, algorithms
The first step is to create the necessary types. Usually it is fitness and the individual.
creator.create("FitnessMin", base.Fitness, weights=(-1.0,))
creator.create("Individual", list, fitness=creator.FitnessMin)
Next, you need to create a toolkit. To do this, you need to set the basic parameters for our algorithm.
Sol_B = 0.02 # [T] average Bz in the solenoids
Sol_B_max = 0.05 # [T] max Bz
Sol_B_min = 0.005 # [T] min Bz
Sol_Num = 9 # quantity
CXPB = 0.4 # cross chance
MUTPB = 0.6 # Mutation probability
NGEN = 100 # Number of generations
POP = 100 # Number of individuals
toolbox = base.Toolbox()
toolbox.register("attr_float", random.gauss, Sol_B, ((Sol_B_max - Sol_B_min)/2)**2)
toolbox.register("individual", tools.initRepeat, creator.Individual, toolbox.attr_float, n=Sol_Num)
toolbox.register("population", tools.initRepeat, list, toolbox.individual)
Create a fitness function.
def evalution_envelope(individual):
for x in range(Sol_Num):
accelerator.Bz_beamline['Sol. %.d'%(x+1)].max_field = individual[x]
accelerator.compile()
simulation = kv.Simulation(beam, accelerator)
simulation.track()
tuple(envelope_mod)
tuple(simulation.envelope_x(accelerator.parameter))
sqerrors = np.sqrt((envelope_mod-simulation.envelope_x(accelerator.parameter))**2)
return sum(sqerrors)/len(accelerator.parameter),
toolbox.register("evaluate", evalution_envelope)
toolbox.register("mate", tools.cxUniform, indpb=MUTPB )
toolbox.register("mutate", tools.mutGaussian, mu=0, sigma=((Sol_B_max - Sol_B_min)/2)**2, indpb=MUTPB)
toolbox.register("select", tools.selTournament, tournsize=NGEN//3)
Logbook.
stats_fit = tools.Statistics(lambda ind: ind.fitness.values)
mstats = tools.MultiStatistics(fitness=stats_fit)
mstats.register("avg", np.mean)
mstats.register("std", np.std)
mstats.register("min", np.min)
mstats.register("max", np.max)
logbook = tools.Logbook()
population = toolbox.population(n=POP)
pop, logbook = algorithms.eaSimple(population, toolbox, cxpb=CXPB, mutpb=MUTPB, ngen=NGEN, stats=mstats, verbose=True)
fitness
--------------------------------------------------------------------------
gen nevals avg gen max min nevals std
0 100 0.0373577 0 0.0408331 0.0337452 100 0.00113532
1 82 0.0348016 1 0.0379858 0.0299872 82 0.00134257
2 69 0.0317311 2 0.0355503 0.0268419 69 0.00158446
3 70 0.0284586 3 0.0310798 0.0258454 70 0.00116153
4 77 0.0262835 4 0.028602 0.0245999 77 0.00073413
5 72 0.0248689 5 0.0268379 0.0234427 72 0.000541174
6 84 0.0237668 6 0.0256165 0.0221611 84 0.00067109
7 73 0.0225147 7 0.0241554 0.0203067 73 0.000610466
8 88 0.0210856 8 0.0235622 0.0194378 88 0.000755119
9 80 0.0197334 9 0.0209437 0.0190342 80 0.000337098
10 81 0.0191692 10 0.0204253 0.0183268 81 0.00035722
11 75 0.0185557 11 0.019661 0.0178986 75 0.000283725
12 78 0.0181075 12 0.0190688 0.0175483 78 0.00029574
13 72 0.0177022 13 0.018703 0.0172446 72 0.000248748
14 75 0.0174452 14 0.0183427 0.0169873 75 0.000190804
15 70 0.017232 15 0.0178082 0.0169012 70 0.000181106
16 79 0.0170371 16 0.0180127 0.0167734 79 0.000208848
17 80 0.0168772 17 0.0176019 0.0165999 80 0.000167511
18 80 0.0167085 18 0.0175836 0.0164198 80 0.000174468
19 77 0.0165316 19 0.0171106 0.0162831 77 0.000152431
20 76 0.0163782 20 0.0168837 0.0160568 76 0.000171506
21 69 0.0161959 21 0.0170411 0.015828 69 0.000194345
22 77 0.0159477 22 0.0166562 0.0156399 77 0.000157436
23 79 0.0158229 23 0.0184114 0.0155106 79 0.000314105
24 80 0.0156802 24 0.0167603 0.0153466 80 0.000234712
25 72 0.0154841 25 0.0165787 0.0152393 72 0.000184083
26 74 0.0153536 26 0.0160787 0.0150713 74 0.000201229
27 83 0.0152175 27 0.0160113 0.0147709 83 0.000237473
28 79 0.0149943 28 0.0159486 0.014535 79 0.00027873
29 80 0.0147364 29 0.0155165 0.0143068 80 0.000219007
30 78 0.0145096 30 0.0155232 0.01421 78 0.000219074
31 76 0.0143674 31 0.0162176 0.0141153 76 0.000292944
32 77 0.0142465 32 0.0154183 0.0139755 77 0.000228094
33 74 0.0141755 33 0.016872 0.0137429 74 0.000370584
34 65 0.0140263 34 0.0165405 0.0135535 65 0.000369079
35 79 0.0138775 35 0.0165023 0.0134757 79 0.000469816
36 78 0.0136499 36 0.0165048 0.0132913 78 0.00036574
37 77 0.0135281 37 0.0162187 0.0131399 77 0.000370037
38 72 0.0133894 38 0.0161935 0.013018 72 0.000407104
39 74 0.0132855 39 0.0151958 0.0129085 74 0.000356725
40 73 0.0132202 40 0.0158132 0.0127831 73 0.000502361
41 78 0.0131469 41 0.0154469 0.0126621 78 0.000549534
42 72 0.0128525 42 0.0153473 0.0125449 72 0.000371909
43 81 0.0128408 43 0.0143709 0.0124426 81 0.00037498
44 80 0.0128018 44 0.0143546 0.0122802 80 0.00042712
45 76 0.0126884 45 0.0149749 0.0122105 76 0.000484442
46 74 0.0124913 46 0.0141759 0.0121807 74 0.000374844
47 84 0.0124814 47 0.0150409 0.012149 84 0.000478495
48 65 0.012378 48 0.0143345 0.0120466 65 0.000396209
49 77 0.0123797 49 0.0141054 0.0119723 77 0.000465145
50 66 0.0122275 50 0.0136186 0.0119299 66 0.000324548
51 77 0.0122757 51 0.0142704 0.0118622 77 0.000472376
52 74 0.0121928 52 0.0138265 0.0118082 74 0.000460488
53 73 0.0121423 53 0.0145869 0.0117309 73 0.000487374
54 70 0.0120654 54 0.0132641 0.0116092 70 0.000405956
55 77 0.012012 55 0.0137579 0.0115895 77 0.00050723
56 73 0.0118692 56 0.0141939 0.0115563 73 0.000437811
57 83 0.0118798 57 0.0139667 0.0114851 83 0.000426248
58 71 0.0117967 58 0.01344 0.0114796 71 0.000419319
59 72 0.0117301 59 0.0145933 0.0114334 72 0.000445674
60 78 0.0116524 60 0.0135045 0.0113808 78 0.000333071
61 78 0.0116611 61 0.0132638 0.0113299 78 0.000437407
62 78 0.0116445 62 0.0140102 0.0113001 78 0.000467812
63 80 0.0116662 63 0.0138093 0.0112541 80 0.000496356
64 78 0.0115682 64 0.0126411 0.0112403 78 0.000360796
65 73 0.0115044 65 0.0133941 0.0112293 73 0.000428872
66 81 0.0114277 66 0.0134346 0.0112152 81 0.000315043
67 72 0.0114574 67 0.0132544 0.0111495 72 0.000390321
68 81 0.0114764 68 0.0135241 0.0110932 81 0.000486222
69 75 0.011434 69 0.0132443 0.0110874 75 0.000469529
70 74 0.0113903 70 0.0129446 0.0109944 74 0.000420948
71 80 0.0112841 71 0.0132937 0.0109944 80 0.000408004
72 75 0.0112891 72 0.0133998 0.010978 75 0.000465794
73 79 0.0112265 73 0.0122116 0.0109464 79 0.00029769
74 80 0.0112526 74 0.0129213 0.0108979 80 0.000417258
75 71 0.0112418 75 0.0128844 0.0108979 71 0.000447559
76 73 0.0111925 76 0.0138475 0.0108402 73 0.000519714
77 78 0.0111465 77 0.0132176 0.010835 78 0.000422602
78 79 0.0112091 78 0.0133698 0.0107964 79 0.000558782
79 73 0.0110862 79 0.0131931 0.0107964 73 0.000465272
80 67 0.011036 80 0.0127483 0.0107964 67 0.000386788
top = tools.selBest(pop, k=10)
gen = np.array(logbook.select("gen"))
fit_min = np.array(logbook.chapters["fitness"].select("min"))
fit_max = np.array(logbook.chapters["fitness"].select("max"))
fit_avg = np.array(logbook.chapters["fitness"].select("avg"))
for x in range(Sol_Num):
accelerator.Bz_beamline['Sol. %.d'%(x+1)].max_field = top[0][x]
accelerator.compile()
simulation = kv.Simulation(beam, accelerator)
simulation.track()
z_Bz_gen= hv.Area((accelerator.parameter,accelerator.Bz(accelerator.parameter)), kdims=[dim_z], vdims=[dim_Bz])
z_r_gen = hv.Area(((accelerator.parameter,simulation.envelope_x(accelerator.parameter)*1e3)), kdims=[dim_z], vdims=[dim_r], group='Beam')
(z_r_gen*z_env+z_Bz_gen).cols(1)
Коррекция равновесной орбиты в ускорителе заряженных частиц с применением матрицы отклика и нейронных сетей
Резюме
Литература
[1] Lawson John David. The physics of charged-particle beams. — 1977
[2] SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python / Pauli Virtanen, Ralf Gommers, Travis E. Oliphant et al. // Nature Methods. — 2020. — Vol. 17. — P. 261–272.
[3] Ivanov AV, Tiunov MA. ULTRASAM-2D code for simulation of electron guns with ultra high precision // Proceeding of EPAC-2002, Paris. — 2002. — P. 1634–1636.
[4] Fedorov VV, Nikiforov DA, Petrenko AV. KENV Kapchinsky Envelope code. — 2019. — https://github.com/fuodorov/kenv.
[5] Deap: A python framework for evolutionary algorithms / Fran¸coisMichel De Rainville, F´elix-Antoine Fortin, Marc-Andr´e Gardner et al. // Proceedings of the 14th annual conference companion on Genetic and evolutionary computation. — 2012. — P. 85–92.
[6] Федоров В. В., Никифоров Д. А., Петренко А. В. KENV, Свидетельство о государственной регистрации программы для ЭВМ № 2024611244 от 18.01.2024. — 2024. — URL: https://fips.ru/EGD/ f842405a-9bc0-422f-8c1e-c945356a93f9.
[7] Никифоров Д. А. Исследование динамики пучка электронов в мощном линейном индукционном ускорителе с фокусировкой на сосредоточен- 39 ных элементах : Дисс. . . кандидата наук ; ИЯФ СО РАН. — 2023. — С. 1–94. — URL: https://inp.nsk.ru/images/Nikiforov_disser.pdf.
[8] High-current electron-beam transport in the LIA-5 Linear Induction Accelerator / DA Nikiforov, MF Blinov, VV Fedorov et al. // Physics of Particles and Nuclei Letters. — 2020. — Vol. 17. — P. 197–203.
[9] High Current Electron Beam Transport and Focusing at the Linear Induction Accelerator / S.L. Sinitsky, E.S. Sandalov, D.I. Skovorodin et al. // 2020 IEEE International Conference on Plasma Science (ICOPS). — 2020. — P. 191–191.
[10] Investigation of high current electron beam dynamics in linear induction accelerator for creation of a high-power THz radiation source / D.A. Nikiforov, A.V. Petrenko, S.L. Sinitsky et al. // Journal of Instrumentation. — 2021. — nov. — Vol. 16, no. 11. — P. P11024. — URL: https://dx.doi.org/10.1088/1748-0221/16/11/P11024.
[11] Logatchev Pavel, Malyutin Dmitriy, Starostenko A. Application of a lowenergy electron beam as a tool of nondestructive diagnostics of intense charged-particle beams // Instruments and Experimental Techniques. — 2011. — 01. — Vol. 51. — P. 1–27.
[12] Martin Robert C. Clean architecture. — 2017.
[13] Shalloway Alan, Trott James R. Design patterns explained: A new perspective on object-oriented design, 2/E. — Pearson Education India, 2005.
[14] Meyer Bertrand. Object-oriented software construction. — Prentice hall Englewood Cliffs, 1997. — Vol. 2. 40
[15] UnitTest Unit testing framework. — URL: https://docs.python.org/ 3/library/unittest.html (online; accessed: 2024-01-01).
[16] PyTest helps you write better programs. — URL: https://github.com/ pytest-dev/pytest/ (online; accessed: 2024-01-01).
[17] Hodges Jr JL. The significance probability of the Smirnov two-sample test // Arkiv f¨or matematik. — 1958. — Vol. 3, no. 5. — P. 469–486.
[18] Merkel Dirk et al. Docker: lightweight linux containers for consistent development and deployment // Linux j. — 2014. — Vol. 239, no. 2. — P. 2.
[19] GitHub Actions is generally available. — URL: https://github.blog/ changelog/2019-11-11-github-actions-is-generally-available/ (online; accessed: 2024-01-01).
[20] Flake8 is a python tool that glues together pycodestyle, pyflakes, mccabe, and third-party plugins to check the style and quality of some python code. — URL: https://github.com/PyCQA/flake8 (online; accessed: 2024-01-01).
[21] PyLint It’s not just a linter that annoys you! — URL: https://github. com/pylint-dev/pylint (online; accessed: 2024-01-01).
[22] Numba A Just-In-Time Compiler for Numerical Functions in Python. — URL: https://github.com/numba/numba (online; accessed: 2024-01- 01).
[23] Fedorov VV, Nikiforov DA. REDPIC Relativistic Difference Scheme Particles-In-Cell. — 2020. — https://github.com/fuodorov/redpic.
[24] Федоров В. В., Никифоров Д. А. REDPIC, Свидетельство о государственной регистрации программы для ЭВМ 41 № 2023688768 от 25.12.2023. — 2023. — URL: https://fips.ru/ EGD/4182c66d-0ac9-4330-af31-cb2154704aa9.
О себе
Меня зовут Федоров Вячеслав Васильевич, я опытный разработчик программного обеспечения с глубокими знаниями в области физики и вычислительной математики. На протяжении нескольких лет я работаю в Институте ядерной физики им. Будкера, где занимаюсь разработкой наукоемкого прикладного программного обеспечения на языках высокого уровня Python и C++ для решения различных задач. Моя основная работа сосредоточена на моделировании динамики заряженных частиц в сложных электромагнитных полях, а также на внедрении алгоритмов машинного обучения для оптимизации и настройки ускорительных комплексов.
Мой опыт также включает работу в международной компании по разработке ПО и веб-приложений SIBERS, где я руководил командой разработчиков в создании ПО на основе микросервисной архитектуры для государственной организации, оказывающей финансовые услуги. Я активно участвовал в разработке дополнительных модулей для статического анализа кода для различных сред разработки, а также был ведущим разработчиком приложения для врачей, предназначенного для распознавания и присвоения кодов болезней в медицинских картах пациентов с использованием бессерверных вычислений и алгоритмов машинного обучения. Я внедрял процессы автоматизированного тестирования, непрерывной интеграции и доставки кода, проводил обзор и оценку кода, а также подготовил и прочитал полугодовой обучающий курс «Микросервисные масштабируемые веб-сайты» для команды.
Ранее я принимал участие в проектах Роскосмоса, в том числе в разработке ПО на языке C++ для инфракрасного датчика горизонта с использованием платформы Arduino для сверхмалого космического аппарата НГУ «Норби», успешный запуск которого состоялся в 2020 году.
У меня есть диплом бакалавра НГУ в области физики пучков заряженных частиц и физики ускорителей. Я прошёл курсы повышения квалификации по разработке и эксплуатации ПО на Python и C++, алгоритмам и структурам данных, системному администрированию и обеспечению надёжности информационных систем от «Образовательных технологий Яндекса», а также основы искусственного интеллекта и машинного обучения от НГУ.
Мои технические навыки включают: отличное владение языками программирования Python и C++, разнообразными фреймворками; работу с асинхронным и параллельным кодом; проектирование ПО, веб-приложений и микросервисов; создание документации; работу с реляционными базами данных и NoSQL-хранилищами; управление очередями сообщений и задач; владение методологиями непрерывной интеграции и доставки кода, автоматизации процессов сборки, настройки и развёртывания ПО. Мой опыт позволяет ускорять процессы производства IT-продуктов за счёт поиска и устранения «узких» мест, автоматизировать процесс разработки и развёртывания приложений, контейнеризировать приложения и размещать их в облачных сервисах. Я использую актуальные инструменты для обеспечения качества, скорости и стабильности приложений, управляю инфраструктурой в парадигме Infrastructure as Code, сокращая время команды на развёртывание и масштабирование, а также налаживаю коммуникацию между участниками процесса разработки продукта: службой эксплуатации, разработчиками, заказчиками от бизнеса и многими другими.